METODE
CANTITATIVE DE STABILIRE A AMPLASARII UNITATILOR DE
PRODUCTIE
1 Metoda medianei simple
Metoda pragului de rentabilitate
Metoda medianei simple
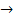 presupune
alegerea localizarii optime pe baza minimizarii cheltuielilor de
transport luand in considerare incarcatura mediana. Calculele se
fac considerand ca volumul incarcaturilor este transportat de
rentangulare si toate deplasarile se fac pe directia est vest
sau nord sud, iar miscarile diagonale nu sunt luate in considerare
.
presupune
alegerea localizarii optime pe baza minimizarii cheltuielilor de
transport luand in considerare incarcatura mediana. Calculele se
fac considerand ca volumul incarcaturilor este transportat de
rentangulare si toate deplasarile se fac pe directia est vest
sau nord sud, iar miscarile diagonale nu sunt luate in considerare
.
Modelul medianei simple ofera o
solutie optima.
In cadrul problemelor propuse vor fi
cunoscute urmatoarele :
Li 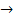 numarul de
incarcaturi care vor fi expediate anual intre fiecare unitate
existenta Fi si noua unitate optima;
numarul de
incarcaturi care vor fi expediate anual intre fiecare unitate
existenta Fi si noua unitate optima;
Fi
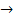 unitatile existente;
unitatile existente;
(Xi,
Yi) 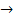 coordonatele pentru
fiecare unitate existenta Fi;
coordonatele pentru
fiecare unitate existenta Fi;
Ci 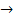 costul asociat mutarii unei incarcaturi cu
o unitate de distanta intre unitatea Fi si noua
unitate optima.
costul asociat mutarii unei incarcaturi cu
o unitate de distanta intre unitatea Fi si noua
unitate optima.
(X0,
Y0) 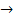 coordonatele noii
unitati care asigura costul minim.
coordonatele noii
unitati care asigura costul minim.
Costul
total de transport
CT =  *
* 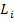 *
* 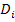 unde:
unde:
Di =
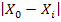 +
+ 
Di =
distanta intre fiecare unitate existenta si noua unitate
optima.
Scopul
demersului nostru prin folosirea acestei metode este gasirea valorilor X0, Y0 (noua
fabrica) care are ca si rezultat costuri minime de transport. Pentru
aceasta, parcurgem urmatoarele 4 etape:
Identificare
valorii mediane a incarcaturilor Zi mutate;
Determinarea
coordonatei X0 a unitatii existente care trimite (sau primeste
)incarcarea mediana;
Determinarea
coordonatei Y0 a unitatii existente care trimite (sau
primeste )incarcarea mediana;
Calculul
costul total de transport minim CT = 
Problema nr. 10
Se doreste amplasarea unei noi fabrici
care va primi anual loturi de materii prime din doua surse : F1 si F2 . Noua fabrica va crea bunuri finite care trebuie expediate catre 2
depozite de distributie F3 si
F4 . In tabelul de mai jos sunt redate amplasarile celor 4
unitati existente, numarul incarcaturilor transportate si costurilor
pentru a muta o incarcatura cu o unitate de distanta.
Se cere:
Determinarea coordonatelor noii fabrici pentru
o minimizare costurile anuale de transport;
Costul anual de transport pentru noua fabrica.
|
Unitatea
Existenta
|
Incaracaturi
Anuale Intre Fi SI Noua Fabrica (Li)
|
Costul
pentru a muta o incarcatura cu o unitate de distanta
(Ci)
|
Amplasarea
coordonatelor
(Xi,
Yi) ale Fi
|
|
F1
|
|
|
|
|
F2
|
|
|
|
|
F3
|
|
|
|
|
F4
|
|
|
|
|
TOTAL
|
|
|
|
Rezolvare
Parcurgerea celor 4 etape
de rezolvare:
Identificarea
incarcaturii mediane 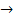 numarul total
de incarcaturi mutate spre si de la noua fabrica este
numarul total
de incarcaturi mutate spre si de la noua fabrica este 
Numarul
incarcaturii mediane este numarul din mijloc al lui 2605,
adica 1303.
OBS.  daca
numarul total de incarcaturi ar fi par, am lua in considerare
numere din mijloc .
daca
numarul total de incarcaturi ar fi par, am lua in considerare
numere din mijloc .
Determinarea
coordonatei X0 a incarcaturii mediane 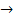 X0 =
20.
X0 =
20.
Incepand din origine (0,0) avansam spre dreapta pe axa OX pana
la cel mai apropiat Xi . Acesta este X2 =10 si
corespunde amplasarii fabricii F2. Numarul total de
incarcaturi pana la F2 este 900 din tabel.
Incarcatura mediana este 1303 si nu se incadreaza in
intervalul 1-900. Continuam rationamentul.
Avansam spre urmatorul Xi pe scara OX. Acesta este
Xi =20. Incarcaturile 901 -1655(1655 s-a obtinut prin
L1 + L2 ) sunt expediate de fabrica F1 de la
amplasamentul cu coord. X1 = 20. Incarcatura mediana 1303 se afla in intervalul 901
1655, asadar X0 = 20 este amplasamentul dorit al coordonatei X
pentru noua fabrica.
Determinarea
coordonatei Y0 a
incarcaturii mediane Y0
=40
Acum luam in considerare directia y a miscarilor
incarcaturii. Incepem de la origine (0,0) si avansam in sus
de-a lungul axei OY. Miscarile in directia y incep cu expedierea
incarcaturilor, 1-755 de catre F1 de la amplasamentul
y=30.
Incarcatura mediana 1303 nu se
afla in intervalul 1-755.
Continuam rationamentul.
Incarcaturile 765 1655 sunt expediate de catre F2
desi amplasamentul y = 40. Incarcarea medianei 1303 se
gaseste in intervalul 765 1655 si y0 = 40 e
coordonata dorita pentru noua
fabrica.
OBS Amplasamentul optim al fabricii X = 20, Y =
40 are ca rezultat minimizarea costurilor anuale de transport pentru
aceasta retea de unitati.
Calculul
costului total de transport pentru unitatea optima
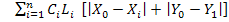 = 45.550 usd
= 45.550 usd
Se determina
conform datelor stabilite in urmatorul tabel
|
Unitatea
existenta Fi
|
Coordonata
Xi
a
Fi
|
Coordonata
Yi
a
Fi
|
Distante intre Fi
si noua fabrica
|
Li
|
Ci
|
CTi
CT=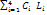 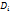
|
|
Directia X
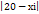
|
Directia y
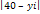
|
Distanta totala
Di
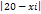 
|
|
F1
|
|
|
|
|
|
|
|
|
|
F2
|
|
|
|
|
|
|
|
|
|
F3
|
|
|
|
|
|
|
|
|
|
F4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TOTAL
|
|
CT = 7550 + 9000 + 9000 + 20.000 = 45.550 usd
1 Probleme propuse pentru metoda medianei simple
Problema 11
Este cautat un amplasament
pentru o fabrica temporara care va furniza ciment pentru trei amplasament
existente de constructii : in centru, la un complex comercial si
intr-o suburbie. Locatiile amplasamentelor existente si
incarcaturile care trebuie livrate catre fiecare sunt :
|
Amplasamentul de livrare (Si)
|
Coordonatele
(Xi, yi) in mile
|
Incarcaturile catre noua fabrica (Li)
|
Costul de mutare a unei
incarcaturi cu o mila (Ci)
|
|
S1 Centru
|
|
|
10 usd
|
|
S2 Complex comercial
|
|
|
10 usd
|
|
S3 Suburbie
|
|
|
10 usd
|
|
|
TOTAL 101
|
|
Determinati cel mai bun amplasament
pentru fabrica de ciment. Care vor fi costurile totale de expediere rezultate ?
Rezolvare
Incarcatura mediana =S1 (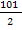 = 50,5
= 50,5 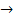 51)
51)
X = 10 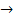 43 incarcaturi 51 (1
43)
43 incarcaturi 51 (1
43)
X = 20 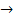 75 incarcaturi 51
75 incarcaturi 51  (44 75)
(44 75) 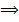 X0 =20
X0 =20
Y = 10 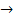 22 incarcaturi 51 (
1 - 22 )
22 incarcaturi 51 (
1 - 22 )
Y = 20 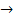 58 incarcaturi 51
(23 58)
58 incarcaturi 51
(23 58) 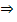 Y0 =20
Y0 =20
Si
|
Distanta fata de noua
fabrica
|
Ci
|
Li
|
Cti
|
|
20 - xi
|
20 - yi
|
Di
|
|
S1
|
|
|
|
|
|
|
|
S2
|
|
|
|
|
|
|
|
S3
|
|
|
|
|
|
|
Problema 12
Se cere sa se stabileasca
amplasamentul optim al unei intreprinderi care minimizeaza costurile de
transport cunoscand ca viitoarea intreprindere se va aproviziona cu
materii prime de la doua surse A1 si A2 , iar produsele
sunt vandute catre 3 centre de consum C1, C2, C3. Se dau in tabel amplasarea centrelor
de aprovizionare si de consum si greutatile transportate.
|
Centre
de aprovizionare si de consum
|
Greutati anuale transportate
intre centre si viitoare intreprindere (Gi) (tone)
|
Tarif de
transport
(ti) lei/tkm
|
Coordonatele
(Xi, Yi) de amplasament al centrelor
|
|
A1
|
|
|
|
|
A2
|
|
|
|
|
C1
|
|
|
|
|
C2
|
|
|
|
|
C3
|
|
|
|
|
Total
|
|
|
|
METODA PRAGULUI DE RENTABILITATE
Aceasta metoda numita
si analiza de echilibru identifica nivelul de productie care
trebuie atins pentru a recupera prin venituri toate costurile de operare.
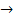 se aplica
in cazul in care costurile variabile unitare (Cv), precum si costurile fixe (CF) se modifica in
functie de localizarea intreprinderii.
se aplica
in cazul in care costurile variabile unitare (Cv), precum si costurile fixe (CF) se modifica in
functie de localizarea intreprinderii.
Pragul
de rentabilitate (Break even), punctul critic sau punctul de
echilibru este dat de acel volum al productiei pentru care veniturile
totale (Vt) sunt egale cu valoarea costurilor totale (Ct).
Acest volum de productie se
noteaza cu qcrt sau qmin.
Costurile fixe totale sunt acelea care
nu se modifica cu variatia volumului de productie, iar cele
variabile totale sunt dependente de variatia volumului productiei.
Cv = cv * q q =
productia
Cv = costuri variabile totale
cv = costuri variabile unitare
Ct = CF + CV = CF + cv*q
Veniturile obtinute din vanzarea
productiei sau cifra de afaceri din activitatea de baza sunt de date
de relatia:
Vt = Pv
*q , Pv = pret de vanzare
unitar.
Pragul de rentabilitate se
obtine la acel volum al productiei pentru care are loc egalitatea
Vt = Ct
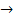 pentru o
productie omogena, pragul de rentabilitate se exprima in
unitati naturale sau fizice (tone, bucati, m2)
pentru o
productie omogena, pragul de rentabilitate se exprima in
unitati naturale sau fizice (tone, bucati, m2)
|
qcrt = 
|
 Vt = Ct
Vt = Ct
Pv*q = CF +
cv *q 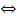 q (Pv
cv) = CF
q (Pv
cv) = CF 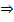
 pentru o
productie eterogena, pragul de rentabilitate trebuie calculat in
unitati valorice aflandu-se volumul critic al activitatii
sub forma cifrei de afaceri critice (CAcrt)
pentru o
productie eterogena, pragul de rentabilitate trebuie calculat in
unitati valorice aflandu-se volumul critic al activitatii
sub forma cifrei de afaceri critice (CAcrt)
Vt
= Ct
CA = CF +
CV 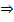 CF = CA Cv | : CA
CF = CA Cv | : CA
|
CAcrt = 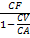
|

Problema 13
Pentru amplasarea unei
intreprinderi au fost selectate 3 localitati L1,
L2, L3, care au structuri de costuri asa cum se
prezinta in tabel, pentru un produs care se apreciaza ca va fi vandut cu 2 milioane lei.
Se cere:
a) Sa se gaseasca
amplasarea cea mai economica pentru
un volum anual de productie q=
10.000 buc;
b) Profitul coresp.
acestei localizari.
q = 10.000
bucati
|
Localitate
|
Costuri fixe pe an CF (mld lei)
|
Costuri variabile pe unitatea de
produs cv (mil lei)
|
|
L1
|
|
|
|
L2
|
|
|
|
L3
|
|
|
Rezolvare: a) Ct =
CF + Cv
Cv = cv*
q 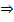 Ct =
CF + cv *q
Ct =
CF + cv *q
Ctl1 = 4
mld +1,5 mil * 10.000 =19 mld lei
Ctl2 = 5
mld + 1,0 mil * 10.000 =15 mld lei
Ctl3 = 8
mld + 0,8 mil * 10.000 =16 mld lei
Amplasamentul cel mai
economic este cel care are costul total minim
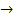 b) Profitul asteptat pentru localizarea
optima este:
b) Profitul asteptat pentru localizarea
optima este:
Profit L2 = Pv * q
Ct
Pr = Vt Ct 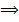 Profit = 2 mil
*10.000 -15 mld = 5mld lei
Profit = 2 mil
*10.000 -15 mld = 5mld lei
Raspunsuri : a) Locatia optima L2
b profitul estimat al locatiei optime = 5
mld. lei
Problema
14
Amplasamentul A are costuri fixe
anuale CF = 300.000 lei, costuri
variabile unitare cv = 63 lei/buc si venituri de 68 lei /buc.
Costurile fixe anuale ale amplasamentului B sunt CF = 800.000 lei, costurile
variabile unitare sunt 32 lei /unitate si veniturile sunt de 68 lei/ unitate. Volumul de vanzari este
estimat la 25.000 unitati anuale. Care amplasament este cel mai
atractiv pe baza analizei pragului de rentabilitate?
Rezolvare
Pragul de rentabilitate in
unitati fizice este calculat pentru fiecare amplasament astfel:
qcrt =
qcrta = =
= 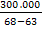 = 60.000
unitati
= 60.000
unitati
qcrtb =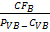 =
= 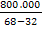 = 22.222
unitati
= 22.222
unitati
OBS E mai atractiv
amplasamentul B, deoarece devine profitabil de la producerea a 22.222
unitati.
Alegerea amplasamentului optim se
poate face si in functie de profitul estimat astfel:
Profit(pierdere) =Vt Ct, q= 25.000 buc
ProfitA = V - C
- C = PVA *
q (CFA + C
= PVA *
q (CFA + C *q)
*q)
=2 mil *25.000 ( 300.000 +
1.575.000) = -175.000
ProfitB = V - C
- C = Pvb*q
(CFB + C
= Pvb*q
(CFB + C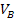 *q)
*q)
= 2 mil *25.000 (800.000 + 800.000)
=100.000 lei
OBS Si
in acest caz, amplasamentul B este cel mai atractiv deoarece se obtine
profit nu pierdere, ca in cazul A.

