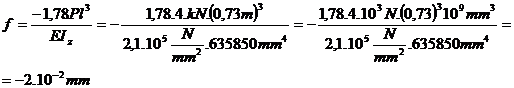Teoremele reciprocitatii lucrului mecanic si a
deplasarilor. Teorema lui Betti
Asupra unui corp
oarecare se aplica doua stari succesive de solicitare, produse
de doua grupe succesive de sarcini, aplicand asupra corpului prima stare
de solicitare , punctele de aplicatie ale fortelor sufera
deplasari, deci fortele produc lucrul mecanic, iar corpul
acumuleaza energia L11 .
Primul indice ( 1 )
indica faptul ca lucrul mecanic este produs de fortele din prima
stare de solicitare, al doilea indice (
1 ) indica deplasarile din prima stare.
Apoi pe corpul
deformat se aplica o a doua
grupa de forte , deci o a doua stare de solicitare , care
cauzeaza o a doua grupa de deplasari, in acest moment,
fortele din a doua stare produse , corespunzator deplasarilor
produse de ele , lucrul mecanic L22
.
In acelasi timp
insa , fortele din prima stare , care se aflau aplicate pe corp,
produc , datorita deplasarilor , produse din a doua stare, lucrul
mecanic L12 , in final
energia acumulata de corp , egala cu lucrul mecanic al fortelor
exterioare, este L11 + L22
+ L12 .
Schimband ordinea de
aplicare a sarcinilor , deci incepand cu a doua si aplicand acelasi
rationament, rezulta lucrul mecanic total
L22 + L11
+ L21 , unde L21 este lucrul mecanic datorita fortelor din a
doua stare si deplasarile produse de prima , in fond energia
totala fiind aceeasi deci : L11
+ L22 + L12 = L22
+ L11 + L21 .
Implica L12 = L21 ; aceasta fiind teorema reciprocitatii lucrului mecanic sau teorema lui Betti care este : daca asupra unui corp deformabil se
aplica doua stari de incarcare succesive, lucrul mecanic
efectuat de fortele ( si cuplurile ) din prima stare cu
deplasarile ( sageti si unghiuri ) din a doua este egal cu
lucrul mecanic efectuat din a doua stare cu deplasarile din prima stare de
incarcare.
Problema nr.9
Sa se calculeze
sageata din punctul D , pentru bara din figura 38 a) , stiind ca
: E = 2,1.105 N/mm2
; F = 4 kN ; l = 0,73 m , sectiunea
transversala fiind circulara cu diametru d = 60 mm.
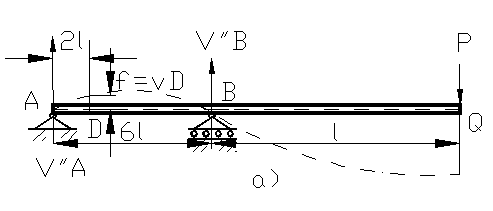

Figura 38
 ; prima stare de
incarcare , se ia incarcarea reala a barei , iar drept a doua
stare se aplica o forta egala cu unitatea ( forta
versor a fortei P ) in
sectiunea unde urmeaza a se afla sageata [ figura 38 cazul b)] .
Deci bara este supusa succesiv la fortele
; prima stare de
incarcare , se ia incarcarea reala a barei , iar drept a doua
stare se aplica o forta egala cu unitatea ( forta
versor a fortei P ) in
sectiunea unde urmeaza a se afla sageata [ figura 38 cazul b)] .
Deci bara este supusa succesiv la fortele  ,
,  este forta versor ( unitate) si se aplica in
sectiunea transversala D. Lucrul mecanic al fortelor din prima
stare de incarcare , adica a fortei P , cu deplasarea
corespunzatoare de la a doua stare este L12 = - Pv ;
este forta versor ( unitate) si se aplica in
sectiunea transversala D. Lucrul mecanic al fortelor din prima
stare de incarcare , adica a fortei P , cu deplasarea
corespunzatoare de la a doua stare este L12 = - Pv ;
v = vQ ( s-a luat cu minus pentru
ca v este in sens invers cu forta
P ) .
Analog , forta versor
( unitara) de la a doua stare cu
deplasarea din dreptul ei de la prima stare da L21 = - 1.f ( semnul minus pentru ca forta unitara s-a luat de sens
contrar sagetii f ) deci : L12 = L21 ;
-Pv = -1.f ; rezulta
ca Pv = 1.f , [Pv] = [1.f ] ; [P] [v] = [1].[f ] ;
[kN] . [m ] = [kN] .
[m] ( forta unitate poate fi : 1 kN
; 1 N ; etc. ) . Pentru bara din figura
38 cazul b) :
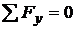 ;
;  ; ecautia de verificare.
; ecautia de verificare.
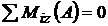 ; 1.2l - VB. 6l =0 ;
; 1.2l - VB. 6l =0 ; 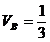 ;
; 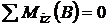 ;
;
- 1.4l +VA.
6l =0 ; 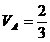 .
.
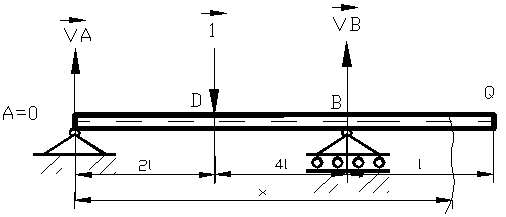
Figura 39
 ; ecautia de verificare,
; ecautia de verificare, 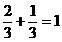 ; este
indeplinita ecautia de verificare.
; este
indeplinita ecautia de verificare.
Aplicam
procedeul Clebsch, pentru calculul sagetilor si a rotirilor, in
cazul nostru trebuie sa determinam rotirea in punctul A ( rotirea in
origine ) , am luat ca origine capatul A ( A = O si aceasta origine ramane
neschimbata pe tot timpul rezolvarii problemei). 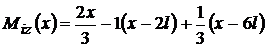 ; este expresia momentului generalizator din
ultima regiune,
; este expresia momentului generalizator din
ultima regiune,  ;
;
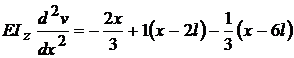


deci, D = 0 . Aflam pe C din a doua
conditie de reazem:
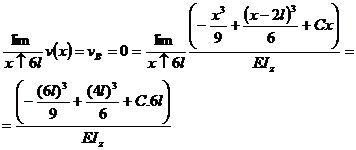 ; rezulta ca ,
; rezulta ca ,
C = 2,22 l2
; 
 ;
; 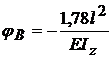 .
.
Din figura 39 portiunea BQ nu este solicitata
deci Miz (x) = 0 ,
aplicam ecuatia fibrei medii deformate pe aceasta regiune
si se obtine:
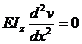 ;
; 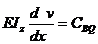 ;
;  ;
;  este ecutia
dreptei BM (ecuatia fibrei medii
deformate) .
este ecutia
dreptei BM (ecuatia fibrei medii
deformate) .
In triunghiul BQM din figura 38 cazul b) aplicam
functiile trigonometrice :
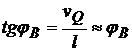 ;
; 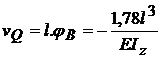 ;
;
sageata in D , fiind fD = f ;  ;
; 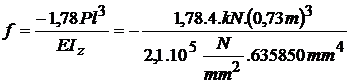 ;
;
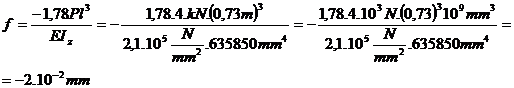




 ; prima stare de
incarcare , se ia incarcarea reala a barei , iar drept a doua
stare se aplica o forta egala cu unitatea ( forta
versor a fortei P ) in
sectiunea unde urmeaza a se afla sageata [ figura 38 cazul b)] .
Deci bara este supusa succesiv la fortele
; prima stare de
incarcare , se ia incarcarea reala a barei , iar drept a doua
stare se aplica o forta egala cu unitatea ( forta
versor a fortei P ) in
sectiunea unde urmeaza a se afla sageata [ figura 38 cazul b)] .
Deci bara este supusa succesiv la fortele  ,
, 
 ;
;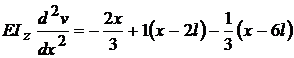


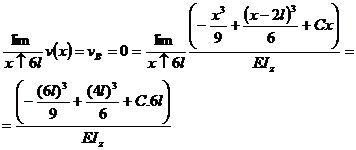 ; rezulta ca ,
; rezulta ca , 
 ;
; 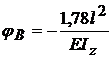 .
.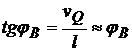 ;
; 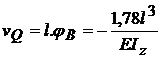 ;
;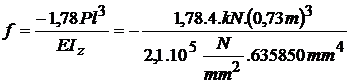 ;
;