Ecuatii echivalente ale dreptei in spatiu

Dreapta in spatiu

Fie R (O; , , ), un reper cartezian ortonormat in spatiul punctual euclidian E₃ = (E₃, V₃, j). Oricarui punct M I E ii putem asocia vectorul de pozitie , unde (x, y, z) I R , coordonatele vectorului in baza vor fi numite coordonatele punctului M.

In spatiul geometric E₃, o dreapta este unic determinata de urmatoarele conditii:

- un punct si de o directie data

- doua puncte distincte

- intersectia a doua plane

1. Dreapta determinata de un punct si o directie

Fie un punct M₀ I E si vectorul nenul I V₃. Vectorul nenul genereaza subspatiul vectorial unidimensional V₁ =

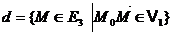
fig. 1

Conditia I V are loc daca si numai daca l I R asa incat = l . Scriind = obtinem

lIR (1)

numita ecuatia vectoriala a dreptei (d) prin punctul M₀ avand directia data de vectorul

Daca proiectam relatia (1) pe axele reperului cartezian R(O, ) obtinem:

(2)

numite ecuatiile parametrice ale dreptei d prin punctul M₀(x₀, y₀, z₀) avand directia data de vectorul

Vectorul = (l, m, n) I V₃ va fi numit vectorul director al dreptei (d) iar coordonatele l, m, n I R vor fi numite parametrii directori ai dreptei (d).

Daca vectorul director este versorul , care formeaza unghiurile

a b g cu axele de coordonate Ox, Oy, Oz, atunci parametrii directori:

cosa, cosb, cosg, coordonatele versorului , se vor numi cosinusurile directoare ale dreptei (d).

Cosinusurile directoare ale unei directii in spatiu satisfac relatia

cos²a cos²b cos²g =

Observatie: ecuatiile (1) sau forma echivalenta (2) guverneaza miscarea rectilinie si uniforma a unui punct material.

Eliminand parametrul l din ecuatiile (2) se obtin ecuatiile:

(3)

numite ecuatiile carteziene canonice (sub forma de rapoarte) ale dreptei d prin punctul M₀(x₀, y₀, z₀) si cu directia data de vectorul = (l, m, n)

Observatie. Ecuatiile canonice se scriu si cand unul sau doi parametri directori sunt nuli, convenind in acest caz ca numaratorul corespunzator este nul si ca ecuatiile sunt date efectiv de egalarea produsului mezilor cu produsul extremilor in proportiile formate.

Dreapta determinata de doua puncte distincte

V₁ =

fig. 2

Cu alte cuvinte un punct M I E apartine multimii suport a subspatiului afin generat de punctele M₁ si M₂, adica M este situat pe dreapta prin cele doua puncte, daca si numai daca vectorii si sunt coliniari. Astfel, multimea punctelor dreptei prin M₁ si M₂ va fi caracterizata de relatia vectoriala

l I R   

sau

(4)

numita ecuatia vectoriala a dreptei prin doua puncte.

In reperul cartezian R (O; ) , considerand M(x, y, z) , M₁(x₁, y₁, z₁) si M₂(x₂, y₂, z₂), vom obtine:

(5)

numite ecuatiile parametrice ale dreptei prin doua puncte.

Observatie: Pentru l I (0, 1) ecuatiile (5) ne procura multimea punctelor de pe dreapta (d) cuprinse intre punctele M₁ si M₂, iar pentru l I R [0, 1] obtinem punctele dreptei (d), puncte exterioare segmentului M₁M Pentru obtinem coordonatele mijloacelor segmentului M₁M

Eliminarea parametrului l I R in ecuatiile (5) sau impunand proportionalitatea coordonatelor a doi vectori coliniari, obtinem

(6)

numite ecuatiile carteziene sub forma canonica ale unei drepte prin doua puncte.