Alternativa Fredholm pentru operatori T= I-U cu U compact

Alternativa Fredholm pentru operatori T= I-U cu U compact

Expunerea ulterioara se bazeaza pe 2 leme simple

Lema IV.2.1. Fie A si B doi operatori liniari continui care aplica spatiul normat X in el insusi. Daca acesti operatori comuta iar operatorul C = AB are invers (bilateral ) atunci si operatorii A si B sunt inversabili

Demonstratie. Sa demonstram intai ca operatorii A si 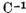comuta, intradevar avem

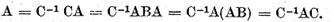
Inmultind aceasta relatie la dreapta cu 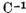obtinem 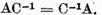Mai departe folosind faptul demonstrat ca A si 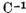comuta putem scrie

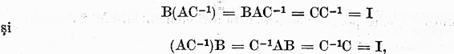
de unde rezulta ca exista Analog se demonstreaza ca exista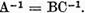

Observatie. Daca operatorul 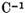este continuu atunci si operatorii si vor fi continui.

Lema IV.2.2. Fie U un operator continuu in spatiul X . Multimea caracteristica a operatorului U si multimea caracteristica 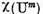a operatorului 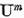sunt legate prin relatia

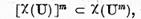
adica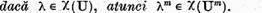

Demonstratie. Sa nota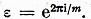m Avem

Daca 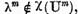atunci punand

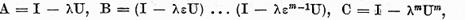
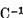rezulta ca exista inversul continuu Prin urmare pe baza observatiei la teorema IV.1.1. exista inversul continuu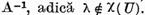

Presupunand ca X este spatiul Banach , ca in subcapitolul IV.1. sa consideram un operator liniar continuu U in X .

Teorema IV.2.3. Sa presupunem ca exista un numar natural m astfel incat operato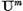rul sa fie compact. Atunci pentru operatorul 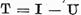este valabila alternativa Fredholm.

Demonstratie. Conform lemei V.2.2 multimea caracteristica 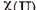consta din puncte izolate, de aceea pe cercul unitate al planului complex se afla doar un numar finit de puncte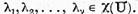

Daca p parcurge multimea tuturor numerelor prime numerele

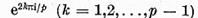
sunt distincte si de aceea pentru 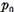suficient de mare

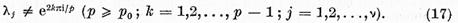
Se poate presupune ca m este un numar prim si ca 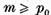. Sa scriem descompunerea

unde

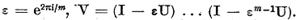
Ca urmare a relatiei (17) operatorii 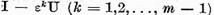sunt inversabili si prin urmare exista operatorul continuu 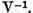Dar atunci

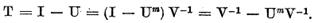
Deoarece operatorul 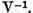este inversabil iar operatorul 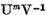este compact se poate aplica teorema IV.1.1 .

Teorema este demonstrata