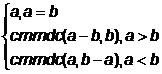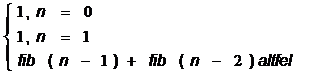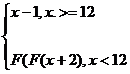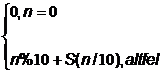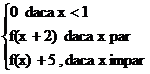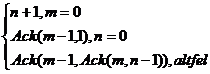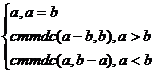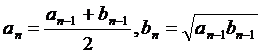Recursivitatea

Recursivitatea este un mecanism general de elaborare a programelor, care consta in posibilitatea ca un subprogram sa se autoapeleze.

Un algoritm recursiv este caracterizat prin:

. Conditie de oprire. Specifica situatia in care rezultatul se poate obtine prin calcul direct fara a mai fi necesara apelarea aceluiasi algoritm.

. Auto-apel. Se apeleaza cel putin o data pentru alte valori ale parametrilor. Valorile parametrilor corespunzatoare succesiunii de apeluri trebuie sa asigure apropierea de satisfacerea conditiei de oprire.

Atentie, recursivitatea trebuie sa fie definita corect, adica sa ai o conditie de oprire. O greseala frecventa este incalcarea acestui principiu.

Primul apel al subprogramului recursiv se realizeaza din exteriorul subprogramului

Exemplu:

Sa se afle al n-lea termen al sirului:

2 pentru n=1

a_n=

a_n-1+5 pentru n>1

iar n se alege dintr-o lista (1,2,,6).

Programul corespunzatoare este:

#include <iostream.h>

int n;

int termen(int n)

void main()

while (n<1 || n>6);

cout<<termen(n); // primul apel realizat din exteriorul subprogramului

}

Subprogramul termen este recursiv- se autoapeleaza din corpul sau. Conditia de oprire este if(n==1) return 2, iar motorul procesului recursiv termen(n-1)+5. Pe stiva se depun adresa de revenire din apel si parametrul n .

Ca urmare a cascadei de auto-apeluri un algoritm recursiv realizeaza de fapt o prelucrare repetitiva, chiar daca aceasta nu este explicita. Un exemplu simplu de prelucrare repetitiva descrisa recursiv este cea corespunzatoare determinarii cmmdc a doua numere naturale nenule, a ≥ b > 0.

Exemplu 1.

Cmmdc(a,b)=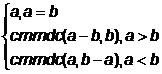

Formula este transcrisa in functia recursiva cmmdc.

int cmmdc(int a,int b)

Programul corespunzator care apeleaza functia este:

#include <iostream.h>

int cmmdc(int a,int b)

void main()

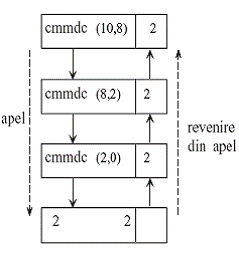
Pentru a ilustra modul de lucru al unui algoritm iterativ poate fi util sa se reprezinta grafic structura de apeluri si reveniri cu returnarea rezultatului obtinut. In cazul unui algoritm recursiv arbitrar structura de apeluri este una ierarhica conducand la un arbore de apel.

In cazul recursivitatii simple arborele de apel degenereaza intr-o structura liniara

Exemplu 2.

Fie fib: NN. Sa se calculeze fib(n), pentru n natural.

Fib(n)=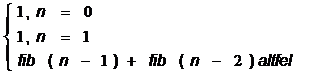

Functia corespunzatoare este urmatoarea

int fib(int n)

Programul aferent este:

#include<iostream.h>

int n ;

int fib(int n)

void main()

Exemplu 3.

Calculul functiei Manna-Pnueli pentru un x intreg.:

F(x)=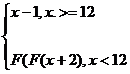

Transpunem formula in functia recursiva:

int manna(int x)

Mai jos este programul ce apeleaza aceasta functie:

# include <iostream.h>

int manna(int x)

void main()

Exemplu 4.

Sa se calculeze recursiv suma cifrelor unui numar natural.

Indicatie: Se izoleaza ultima cifra, iar lui n i se atribuie catul intreg dintre vechea valoare si 10. Astfel gasim o relatie de recurenta, necesara elaborarii variantei recursive:

S(n)=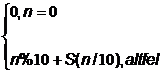

Avem programul:

#include <iostream.h>

int suma(long n)

void main()

Sarcini de lucru:

Se dau urmatoarele definitii recursive:

a) f: N→ N

f(x)=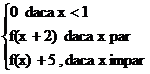

b) g: Z→Z

g(x)=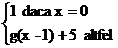

c) h: N→N

h(x)=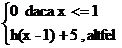

Sunt corecte aceste definitii? Justifica raspunsul.

Completeaza spatiile libere din subprogramul recursiv prezentat mai jos cu  o expresie corespunzatoare, astfel incat in urma apelului f(12) sa se afiseze sirul de valori:

void f(int i)

}

3. Se da urmatorul subprogram:

void scrie (int x)

Ce se afiseaza pe ecran la apelul scrie(12)?

a) 10101

b) 11111

c) 01010

d) 00000.

4. Se da functia lui Ackermann, definita mai jos. Se citesc numerele m si n naturale. Sa se calculeze Ack(m,n).

Ack(m,n)=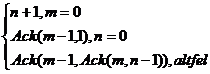

Exemplu: Ack(3,3)=61

Algoritmi de traversare, inversare a unei structuri

Traversarea si inversarea unei structuri inseamna efectuarea unor operatii oarecare asupra tuturor elementelor unei structuri in ordine directa, respectiv in ordine inversa. Variantele recursive sunt mai elegante si concise, decat alte metode. Se pot aplica structurilor de tip tablou, lista, fisier si pot fi o solutie pentru diverse probleme (transformarea unui intreg dintr-o baza in alta, etc). Intr-o forma generala, algoritmii se pot scrie:

functie traversare(tip_element element)




Apelul initial al procedurii se face cu primul element al structurii (exemplu; traversare(1)). De observat importanta ca parametrul formal al celor doua functii sa fie de tip valoare, pentru a nu fi alterat de apelul recursiv

Exemplu

Se citesc si se afiseaza elementele intregi ale unui vector. Cele doua functii recursive, pentru citire si afisare pot incepe cu ultimul element din vector si se termina cu primul.

#include <iostream.h>

int n,v[100];

void citeste(int i)

}

void scrie(int i)

}

void main()

Sarcinia de lucru

Cautarea unui element intr-un sir.

Se da un vector a=(a1,a2,,an) cu n elemente intregi, si un element cu valoarea intreaga x. Folosind functia recursiva gasit(x,i) definita mai jos, sa descri in ordine logica etapele de rezolvare a verificarii existentei elementului x intre componentele vectorului.

gasit(x,i)=

Algoritmi iterativi si recursivi

Axioma

S-a demonstrat matematic ca orice algoritm recursiv poate fi scris iterativ, si reciproc.

Sarcini de lucru

Sa se studieze cele doua metode de rezolvare, iterativa si recursiva, facandu-se o tratare comparativa a lor pentru algoritmul lui Euclid:

Cmmdc(a,b)=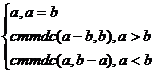

Sirul lui Fibonnacci

Problema nostima:

Cate perechi de iepuri se pot obtine in n luni dintr-o singura pereche stiind ca:

la momentul initial, iepurii din prima pereche sunt nou-nascuti;

fiecare noua pereche de iepuri devine fertila dupa o luna;

fiecare pereche produce o pereche de descendenti in fiecare luna;

nici un iepure nu moare.

Numarul perechilor de iepuri din fiecare luna este descris de sirul:

Fiecare grupa va rezolva cerinta fiecarei fete.

Fata 1: ce tip de problema este?

Fata 2: scrie formula ce rezolva problema.

Fata 3: ce variante avem pentru rezolvare?

Fata 4: scrie varianta cea mai avantajoasa.

Fata 5: argumenteaza alegerea variantei.

Fata 6: enumera un dezavantaj al variantei neutilizate.

Recursivitate indirecta

Se considera sirurile definite recurent astel:

a0=a; b0=b; a,b>0:

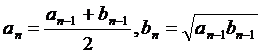
Sa se scrie un program care sa citeasca a,b si n si sa se calculeze an si bn.