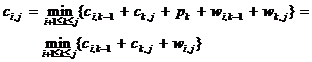Se aplica
atunci cand solutia unei probleme poate fi privita ca rezultat al unei secvente
de decizii.
Exemple:
a) Problema rucsacului --
decizia 1 - xi1 ponderea obiectului i1
--
decizia 2 - xi2 ponderea obiectului i2 . .
b) Interclasarea optimala -- decizia 1 - prima pereche
--
decizia 2 - a doua pereche . .
c) Drumuri
minime de la i la celelalte noduri
--
decizia 1 - in S se adauga i
-- decizia 2 - in S se adauga nodul de distanta
minima . .
Nu toate problemele permit ca la fiecare pas sa se
determine decizia care conduce la solutia optimala.
Ex. drum minim de la i la j
initial
: P =
decizia
1 : care din vecinii lui i vor fi pe
drumul minim ?
O solutie este a se incerca toate variantele
posibile de decizie.
Programarea dinamica reduce numarul de incercari eliminand o
serie de secvente care nu pot fi optimale si aceasta apeland la principiul
optimalitatii:
' O secventa optimala
de decizii are proprietatea ca pornind de la o stare initiala si considerand
prima decizie d1 , secventa de decizii ramase d2, , dn
trebuie sa fie optimala relativ la starea rezultata din prima decizie.'
Problemele care indeplinesc acest principiu sunt
susceptibile de a fi rezolvate prin programare dinamica.
Exemple :
Drum minim de la i la j , doua noduri intr-un graf.
Drumul minim de la i la j este de forma ( i,
i1, i2, , im, j ). Presupunem ca s-a luat
decizia ca i1 este primul
nod dupa i in solutia optimala.
Secventa ( i1, i2, , im, j ) trebuie sa fie
drum minim de la i1 la j , altfel, daca (i1, r1, r2,
, rl, j) este drumul minim de la i1 la j
atunci (i, i1, r1, r2, , rl,
j ) este drumul minim de la i la j si nu ( i, i1, i2,
, im, j ).
Problema rucsacului [0,1]
Problema rucsacului 0/1 se enunta in mod identic cu
problema generala a rucsacului cu observatia ca obiectele
sint indivizibile adica apare restrictia suplimentara asupra
ponderilor xi care trebuie sa fie 0 sau 1.
Formularea problemei:
se cunosc obiectele: i1 , i2 , . . . .in
obiectele au greutatile: w1 , w2 , . . . .wn
obiectele au valorile (profiturile) p1 , p2 , . . . .pn
se considera o capacitate M.
O alegere de obiecte este un vector X=(
x1 , x2 , . . . .xn) unde xi=1 semnifica faptul
ca obiectul i a fost ales iar xi=0 semnifica faptul ca respectivul obiect nu
a fost ales.
Problema consta in determinarea acelei alegeri care nu depaseste
capacitatea dar care maximizeaza profitul, adica:
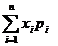 -maxim iar
-maxim iar 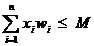
Problema se noteaza cu
: knap(1,n,M). Presupunem ca exista o secventa
X=( x1 , x2 ,
. . . .xn) reprezentind o alegere optimala.
Exista urmatoarele
doua variante:
x1=0 si atunci secventa ( x2 , x3 , . . . .xn) este
optimala pentru problema knap(2,n,M).
x1 =1 si atunci secventa ( x2
, x3 , . . . .xn) este optimala pentru problema
knap(2,n,M-w1).
Se observa ca si in acest caz principiul
optimalitatii se respecta
Fie
s0 starea initiala a
problemei. Presupunem ca sint necesare n decizii d1 , d2 , . . . .dn. Prima decizie poate lua una din valorile multimii D= . Daca decizia d1
ia valoarea ri fie si
starea problemei dupa aceasta decizie, si fie Ri secventa optimala corespunzatoare
subproblemei corespunzatoare starii si.. Daca este indeplinit principiul
optimalitatii secventa optima globala va fi cea mai buna
din secventele: r1R1,
r2R2 , . .., rkRk.
Exemple:
Drum
minim
Se cauta intr-un graf drumul minim de la
nodul i la nodul j. Fie Ei= multimea succesorilor nodului
i si fie drumurile minime
corespunzatoare de la fiecare din acesti succesori la j, anume Rk=
drumul minim de la ik la j, (k=1, . ,s). Atunci drumul minim de la
nodul i la nodul j va fi cel mai mic dintre drumurile (i Rk ), k=1, . ,s.
Problema
rucsacului 0/1
Fie problema knap(1,n,.M) si fie p (M) valoarea profitului maxim pentru aceasta problema.
In general pentru o problema knap(j+1,n,Y) valoarea profitului maxim se
noteaza cu pj(Y). Deoarece x1 ia valori din multimea de decizii D1=, avem:
p (M)=
max (
* )
Daca pentru o problema data este
valabil principiul optimalitatii in starea initiala, atunci se poate
aplica acest principiu si la urmatoarele stari intermediare
Exemple:
Drum
minim
Daca (i, i1, i2, . ..im, j) este drumul minim
de la nodul i la nodul j si ik
este un nod intermediar, atunci secventa
( i, i1, ,i2, . ik) este drum minim de la nodul
i la nodul ik iar secventa (ik,ik+1,
. .j) este drum minim de la nodul ik la nodul j.
Problema
rucsacului 0/1
Fie (x1,x2, . . xn)
o secventa alegere optimala
pentru problema knap(1,n,M). Atunci pentru orice valoare j ( j=1,n) :
(x1,
x2, . ..xj) este solutie optimala pentru problema
knap(1,j, 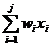 )
)
(xj+1,xj+2,
. xn) este solutie optimala pentru problema knap(j+1, n, M-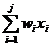 )
)
Relatia anterioara ( * ) se
generalizeaza la
pj(Y) = max
relatia (**) este o recurenta care se poate
calcula stiind ca pn(Y)=0 pentru orice Y numar real.
Exemplele anterioare evidentiaza
recurente de tip "forward" ( in fata). Se pot defini aceste recurente si
in mod "backward".
Exemple
Drum
minim
Daca (i, i1, i2, . ..im, j) este drumul minim
de la nodul i la nodul j, fie Ej'=, |E|=p multimea predecesorilor nodului j. Pentru fiecare predecesor k fie Rk drumul minim de la nodul
i la nodul k. Evident, drumul minim
general va fi cel mai scurt drum din drumurile de forma (Rk j)
pentru k=1, . ,p
Probelema
rucsacului (0/1)
Daca se noteaza cu fi(x) valoarea optima a
problemei knap(1,i,x) se obtin recurentele:
fi
(x)= max i=1,2, . n (*)
Recurentele sint rezolvabile stiind
ca f0(x) = 0  x
x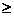 0, f0(x) =
x < 0
0, f0(x) =
x < 0
Problemele
ale caror solutii se pot obtine prin programarea dinamica sunt probleme de
optim. Un prototip de astfel de
problema este urmatorul:
Sa se determine
determine : optim R(x1, . ,xm) (1)
in conditiile in
care acestea satisfac restrictii de forma
g(x1, . ,xm)
? 0 (2)
unde ? I
Prin
optim se intelege de obicei min sau max iar ecuatia (1) se mai
numeste si functie obiectiv. Un alt
prototip este furnizat de digrafurile ponderate, unde R(x1, . ,xm) exprima suma poderilor arcelor x1, . ,xm iar
restrictiile impun ca x1, . ,xm
sa fie drum sau circuit cu anumite proprietati.
Metoda
programarii dinamice propune determinarea valorii optime prin luarea unui
sir de decizii <d1, , dn> numit
si politica, unde decizia di transforma starea (problemei) si-1 in starea si , aplicind principiul
de optim:
Secventa optima de decizii
(politica optimala) care corespunde starii s are proprietatea ca dupa luarea primei decizii, care
transforma starea s in starea s1 , secventa de decizii (politica) ramasa este optima pentru starea s1
De
cele mai multe ori prin stare a problemei se intelege o subproblema. Unei stari i se asociaza o valoare z si se defineste f(z) astfel
incit, daca starea s corespunde
problemei initiale, atunci:
f(z) = optim R(x1, . ,xm) (3)
Principiul
de optim conduce la obtinerea unei ecuatii functionale de forma:
f(z)= optim [H(z,y,f(T(z,y)))] (4)
y
unde
z este valoarea asociata
starii s, T(z,y) calculeaza
valoarea asociata starii s' rezultata
in urma deciziei y iar H exprima algoritmul de calcul al valorii f(z) data de decizia y care
transforma starea s in starea s'.
Dintre toate deciziile care se pot lua in starea s (producind s' ) , se
alege una care da valoarea optima in conditiile in care politica
aplicata in starea s' este si ea
optima.
Ex: Problema rucsacului
pi(Yi) = max
unde pi(Yi ) = valoarea de optim pentru Knap(i+1,n,Yi), Yi= M-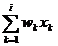
Notatiile din (4) conduc la urmatoarele:
z=i , s=si , f(i) = optim-Knap(i+1,n,Yi)
= pi(Yi). Rezulta: f(i)=f(i+1)+pi+1xi+1
y I , T[i,y]=i+1, s'=si+1 ,
H(i,y,f(T(i,y)))=f(i+1)+ pi+1y
H(i,0,f(T(i,0))) =
H(i,0,f(i+1)] = f(i+1) = pi+1(Yi+1) = pi+1(Yi)
H(i,1 f(T(i,1)))
= H(i,1,f(i+1)] = f(i+1)+pi =pi+1(Yi+1)+pi+1
=pi+1(Yi- wi+1)+pi+1
Rezulta : f(i)= max
Principiul
de optim implica proprietatea de substructura optima a
solutiei, care afirma ca solutia
optima a problemei include solutiile optime ale subproblemelor sale.
Aceasta proprietate este utilizata la gasirea solutiilor
corespunzatoare starilor optime. In general, programele care
implementeaza modelul dat de programarea dinamica au doua
parti:
1. Determinarea valorilor optime date de sirul
de decizii optime, prin rezolvarea ecuatiilor (4)
2. Construirea solutiilor
(valorilor xi care dau optimul) corespunzatoare
starilor optime pe baza valorilor calculate in prima parte, utilizind
proprietatea de substructura optima.
In
general, nu se recomanda scrierea
unui program recursiv care sa
calculeze valorile optime. In cazul programelor recusive, daca in procesul
de descompunere problema subproblema, o anumita subproblema apare de mai multe
ori, ea va fi rezolvata ori de cite ori apare. Asa se procedeaza in
cazul aplicarii metodei Divide-and-Conquer. Este mult mai convenabil ca
valorile optime corespunzatoare subproblemelor sa fie memorate
intr-un tablou si apoi combinate pe baza ecuatiilor (4) pentru a obtine
valoarea optima a unei subprobleme. In acest fel orice subproblema
este solutionata o singura data, iar calcularea valorilor
optime se face de la subproblemele mai mici la cele mai mari ("bottom-up").
Prin memorarea valorilor optime intr-un
tablou se reduce si timpul de calcul pentru optimul unei subprobleme,
datorita accesului la un element dintr-un tablou in O(1) timp.
Complexitatea
algoritmilor care implementeaza metoda programarii dinamice depinde
direct de tipul de recursivitate implicat de recurentele rezultate prin
aplicarea principiului optimalitatii. In cazul recursiei liniare valorile
optime pot fi calculate in timp liniar. In cazul recursiei in cascada
rezulta 2n subprobleme. De obicei in aceste situatii se studiaza posibilitatea redefinirii
starilor astfel incit sa rezulte o recursie liniara
- Metoda greedy utilizeaza proprietatea alegerii
locale: solutia globala optima este construita prin selectii optime locale
-
Metoda programarii dinamice utilizeaza proprietatea de
substructura optima: solutia optima a unei probleme include in
structura sa solutiile optime ale subproblemelor
- Alegerea locala in
cazul metodei greedy nu depinde de alegerile ulterioare, deci metoda greedy nu
are caracter recursiv.
- Proprietate de
substructura optima utilizata in programarea dinamica are
un caracter recursiv: pentru a construi solutia optima a problemei este
necesara cunoasterea solutiilor subproblemelor. Deci rezolvarea problemei implica rezolvarea
subproblemelor.
- Parcurgerea arborelui subproblemelor in
cazul metodei greedy se face in maniera top-down
-
Parcurgerea arborelui subproblemelor in cazul metodei programarii dinamice este
facuta in stil bottom-up
Relatiile de recurenta "backward" rezultate din aplicarea principiului de optim sint urmatoarele:
fi
(x)= max i=1,2, . n (*)
unde fi(x) este valoarea optima a problemei knap(1,i,x).
Recurentele sint rezolvabile stiind ca f0(x) = 0  x
x 0, f0(x) =
x < 0
0, f0(x) =
x < 0
Exemplu : n=3, (w1 , w2
, w3) = (2 , 3 , 4), (p1 , p2 , p3)
= (1 , 2 , 5), M = 6
f0(x)
= 0 g1(x)
= f0(x-w1)+p1 = f0(x-2) + 1































 f1(x) = max g2(x)
= f1(x-w2) + p2 = f1(x-3) + 2
f1(x) = max g2(x)
= f1(x-w2) + p2 = f1(x-3) + 2
f2(x) = max g3(x)
= f2(x-w3) + p3 = f2(x-4) + 5





































f3(x) = max gi(x)
-se obtine din fi printr-o translatie (wi , pi)






































Se observa ca functia fi
este specificata de perechile (w'j , p'j), j = 1,r , unde
w'j sunt abscisele in care fi are un salt , p'j
= f(w'j).
Exemplu f3 caracterizata
de (0,0) , (2,1) , (3,2) , (4,5) , (6,6) , (7,7) , (9,8). Se observa ca functia
este crescatoare, adica w'j < w'j+1  p'j < p'j+1 si ca fi(x) =
fi(w'j) pentru w'j
p'j < p'j+1 si ca fi(x) =
fi(w'j) pentru w'j x<w'j+1 j = 1,r , fi(x) = w'r
x<w'j+1 j = 1,r , fi(x) = w'r
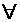 x
x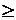 w'r , r = numarul de salturi ale functiei.
w'r , r = numarul de salturi ale functiei.
Fie Si multimea
perechilor care caracterizeaza fi . Atunci Si-1
caracterizeaza fi-1.
Se noteaza cu Ti =
multimea ce caracterizeaza gi(x) = fi-1(x-wi)
+ pi.
Ti
se obtine din Si-1 adunand la fiecare pereche (wi,pi).
Si
se obtine combinand Ti cu Si-1astfel incat sa se obtina
maxim din cele doua functii fi-1 si gi. Combinarea celor
doua multimi Ti si Si-1 se face dupa urmatorul principiu
(principiul dominantei ) :
Fie (w'j,p'j)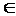 Ti si (w'k,p'k)
Ti si (w'k,p'k)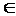 Si-1 sau (w'j,p'j)
Si-1 sau (w'j,p'j)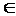 Si-1 si (w'k,p'k)
Si-1 si (w'k,p'k)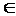 Ti.
Ti.
Daca p'j
< p'k si w'j > w'k , atunci (w'j,p'j)
se elimina.
Pentru exemplul anterior:
S0
= T1
=
S1
= T2
=
S2
= T3
=
S3
=
Observatii 1. In calculul multimilor Si se pot elimina toate
perechile (w,p) cu w > M, deoarece nu se calculeaza fi(x) cu x > M.
2. In conditiile
eliminarilor de la obs.1. valoarea de optim a solutiei este data de ultima
pereche din Sn , (w,p) , anume p este valoarea de optim.
3. Metoda prezentata nu
ofera inca o solutie completa. Cum se deduce solutia (x1 x2
xn) ?
Fie
(w,p) ultima pereche din Sn . Daca (w,p)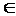 Sn-1 , atunci xn = 0 altfel xn=1. Daca (w,p)
Sn-1 , atunci xn = 0 altfel xn=1. Daca (w,p)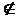 Sn-1, atunci (w-wn, p-pn)
Sn-1, atunci (w-wn, p-pn)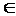 Sn-1 .
Sn-1 .
Se considera (w',p')= (w-wn, p-pn) daca (w,p)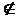 Sn-1 . Altfel (w',p')= (w, p). Se testeaza (w',p')
Sn-1 . Altfel (w',p')= (w, p). Se testeaza (w',p')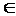 Sn-2 etc.
Sn-2 etc.
Pentru
exemplul anterior:
M =
6 , S3 =
(w,p)
= (6,6) , (6,6)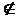 S2 , deci x3 = 1
S2 , deci x3 = 1
(6-w3,
6-p3) = (2,1)
(2,1)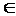 S2 , (2,1)
S2 , (2,1)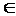 S1
S1 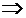 x2 = 0
x2 = 0
(2,1)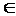 S1 , (2,1)
S1 , (2,1)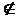 S0
S0 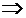 x1 = 1
x1 = 1
dinamic_knapsack(w,p,n,M)
{
S0
= ;
for i =1, . ,n
;
Si =
combine(Ti,Si-1) ;
}
fie (w,p)
ultima pereche din Sn ;
for i=n,n-1, . ,1
if
(w,p)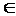 Si-1
Si-1
xi=0;
else
Complexitate
Algoritmul construieste element cu element multimile
S0, S1, . .Sn. In cazul cel mai defavorabil cind nu se elimina nimic
| S0|=1, |S1|=2, . .|Si|=2*|Si-1|=2i,
. . Un calcul simplu
produce urmatorul rezultat
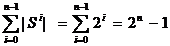
Rezulta
o complexitate de timp si de spatiu exponentiala O(2n)
Metoda
deci este extrem de ineficienta.
Presupunem
ca avem produsul de matrice A1
x A2 x A3 x x An , unde pentru i=1, . ,n, Ai are dimeniunile di si di+1
. Pentru inmultirea acestor matrice numarul total de operatii este d1 *
d2 **dn. Asociativitatea permite o strategie de
solutie care sa minimizeze numarul total de inmultiri.
Exemplu
fie produsul de matrice A1 x
A2 x A3 x A4
de dimensiuni: (100,1) (1,100) (100,1) (1,100)
Consideram
urmatoarele variante de asociere a inmultirilor:
1) (A1 x
A2) x (A3 x A4) 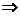 nr.oper. = 10000 + 10000 + 1000000 = 1020000
nr.oper. = 10000 + 10000 + 1000000 = 1020000
2) (A1 x (A2 x A3))
x A4 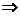 nr.oper. = 100 + 100 +
10000 = 10200
nr.oper. = 100 + 100 +
10000 = 10200
Rezolvarea problemei prin programare dinamica:
Fie
Ai,j = Ai x Ai+1 x x Aj 1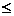 i
i 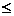 j
j 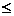 n si cost[ i,j] - costul inmultirii.
n si cost[ i,j] - costul inmultirii.
Observam
cost[ i,i] = 0 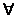 1
1 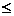 i
i 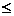 n
n
cost[i, i+1] = di * di+1
* di+2 pentru 1 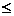 i
i 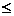 n-1
n-1
Principiul optimalitatii se poate formula astfel:
Pentru un pas general al inmultirii:
(Ai x Ai+1 x x Ak) x ( Ak+1 x Ak+2 x x Aj)
di,di+1 di+1,di+2 dk,dk+1 dk+1,dk+2 dk+2,dk+3 dj,dj+1
cost[
i, j ]= min
i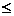 k<j
k<j
Putem calcula acest cost[i,j] in ordinea : j - i = 1
j
- i = 2
..
j
- i = n - 1 pana la cost[1,n].
Construim matricea cost[i,j]. Observam ca matricea
este triunghiulara.
prod(n,d,cost)
cost[ j,i ]= q // q -indicele pt care se realiz.
minimul anterior.
}
}
Pentru exemplul anterior, calculul costului este
urmatorul:
n = 4
d = ( 100, 1 , 100 , 1 , 100 )
cost[1,1] = cost[2,2] = cost[3,3] = cost[4,4] = 0
Pentru k = 1:
i = 1, j = 2, p =1
cost[1,2]
= 0 + 0 + 10000 = 10000
i = 2, j = 3, p = 2
cost[2,3]
= 0 + 0 + 100 = 100
i =
3, j = 4, p = 3
cost[3,4]
= 0 + 0 + 10000 = 10000
Pentru k = 2
:
i = 1 , j = 3
cost[1,3] = min
= min= 200
i = 2 , j = 4
cost[2,4] = min
= min= 200
Pentru k = 3
:
i = 1 , j = 4
cost[1,4] = min
= min= 10200
Complexitate:
Se
poate usor observa ca algoritmul lucreaza in O(n3) , intrucat sunt doua bucle for, plus numarul de comparatii pentru selectia minimului.
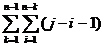 =
= 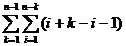 =
= 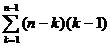 =
= 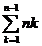 -
- 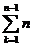 -
-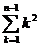 +
+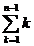
= n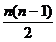 - n. 2n+ n -
- n. 2n+ n - 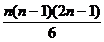 +
+ 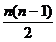 = O(n3)
= O(n3)
Fie A=( a1,
a2, . . an )
secventa sortata crescator cu valori din care se construieste un arbore de
cautare. Se considera ca operatia de cautare se executa cu anumite frecvente.
Anume:
P =
( pi ; pi
- probabilitatea de a fi cautat elementul ai
, i=
1,n )
Q =
( qi ; qi - probabilitatea de a fi
cautat un element x cu proprietatea ai<x<ai+1 , i=0,n )
unde
a0= -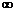 , an+1= +
, an+1= +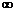 .
.
In
aceste conditii se noteaza:
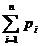 - probabilitatea de
succes
- probabilitatea de
succes
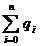 - probabilitatea de
insucces
- probabilitatea de
insucces
iar
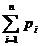 +
+ 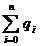 = 1
= 1
Pentru
P si Q date arborele binar de cautare optimal este cel pentru care operatia de
cautare ofera timp mediu minim. Pentru a pune in evidenta timpul mediu se
considera arborele binar de cautare completat cu o serie de pseudonoduri
corespunzatoare intervalelor de insucces, pseudonoduri care se asociaza
pointerilor nuli. In exemplul de mai jos se prezinta un arbore si completatul
sau.
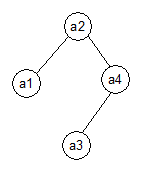
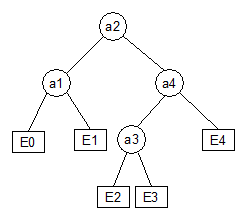
Nodul
Ei corespunde tuturor cautarilor fara succes
pentru valori cuprinse in intervalul
(ai,
ai+1). Timpul unei operatii de cautare pentru un element x este dat de adincimea nodului de
valoare x sau de adincimea
pseudonodului corespunzator intervalului care-l contine pe x.
Costul
unui arbore reprezinta timpul mediu al unei cautari pentru o valoare x , adica
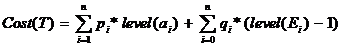
Prin level(a) se noteaza nivelul nodului a si reprezinta numarul de comparatii
efectuate de functia de cautare pe drumul de la radacina
pina la nodul a. Ponderind acest
numar cu probabilitatea de a fi cautat nodul a si efectuind suma pentru
toate nodurile se obtine timpul mediu de cautare cu succes a unui nod. In mod similar se calculeaza
timpul mediu de cautare pentru insucces, cu observatia ca din level(Ei) se scade valoarea 1 deoarece decizia de
apartenenta la un interval nu se face la nivelul pseudonodului ci la
nivelul parintelui sau.
Data fiind secventa de valori A se pot
construi o multime de arbori binari de cautare cu cheile nodurilor din A.
Un arbore binar de cautare optimal este arborele de cost minim.
Din punctul de vedere al programarii
dinamice, construirea unui arbore optimal consta intr-un sir de decizii
privind nodul care se alege ca radacina in fiecare pas.
Fie ( a1,
a2, . ..ak, . . an) secventa de noduri sortata
crescator si presupunem ca in primul pas se alege ca
radacina nodul ak. Conform principiului optimalitatii vom
avea:
subarborele sting L este construit cu secventa ( a1, a2, . ..ak-1)
si clasele (E0,E1,
. Ek-1)
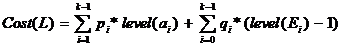
subarborele drept R este
construit cu secventa ( ak+1,
ak+2, . ..an) si clasele (Ek, Ek+1, . ..En)
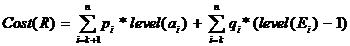
Valoarea level() se calculeaza relativ
la subarborii L, R, respectiv.
Costul
asociat arborelui devine
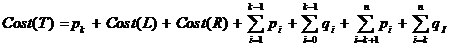 ( * )
( * )
Sumele 
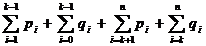 reprezinta valorile
suplimentare care apar datorita faptului ca arborele intreg
reprezinta valorile
suplimentare care apar datorita faptului ca arborele intreg
T introduce un nivel
suplimentar (cel al radacini) fata de subarborii L,R. In continuare relatia (
* ) se rescrie ca :
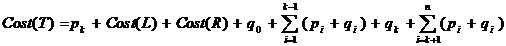 ( ** )
( ** )
Notind 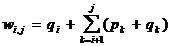 se obtine:
se obtine:
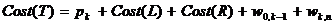 . (
*** )
. (
*** )
Atunci
cind acest cost este minimal el devine egal cu 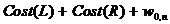 .
.
Principiul
optimalitatii este respectat deoarece subarborii L si R trebuie sa fie
optimi.
Se
noteaza cu ci,j costul unui subarbore optimal Ti,j care are nodurile din
secventa (ai+1, ai+2, . . ..aj) si pseudonodurile din (Ei, Ei+1,
. .Ej ).
Pentru
situatia discutata anterior, in conditiile in care arborele cu nodul radacina ak
este optimal, notatiile devin:
c0,k-1=Cost( L )
ck,n =Cost( R )
Principiul
optimalitatii se scrie astfel:
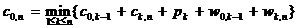 ( **** )
( **** )
Generalizind,
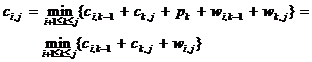
Costul
optimal c0,n se poate
calcula efectiv folosind ultima relatie
de recurenta pentru j-i=1 apoi j-i=2, . . . j-i=n . Valorile initiale sint ci,i=0, wi,i=qi, 0 i n . In plus se foloseste relatia 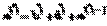
Algoritmul de calcul al
arborelui optimal
opt-bst(P,Q,n)
// (a1,a2, . .an)
secventa de noduri (valori)
// P, Q, secventele de
succes si insucces
// Se calculeaza C=(ci,j)-
costurile, W=(wi,j) si R
matricea de indici ai radacinilor
// ri,j=indicele
nodului radacina al subarborelui optimal format din secventa (ai+1,ai+2, . .aj)
wn,n = qn; rn,n = 0; cn,n
= 0;
for m =2, . ,n
for i =0, . ,n-m
;
// (XXX)
ci,j
= wi,j + ci,k-1 + ck,j ;
ri,j = k ;
}
}
Complexitate
In
mod obisnuit algoritmul lucreaza in timp O(n3) .
Exista o observatie a lui Knuth prin care in linia marcata (XXX) in
algoritm nu se considera intervalul de indici I=[i+1, j] ci
intervalul I=[ ri,j-1 , ri+1,j],
algoritmul lucrind astfel corect in timp O(n2).