Notatia Q (teta)
- Pentru aprecierea
limitei ordinului de marime al timpului de executie al unui
algoritm se utilizeaza notatia Q
- Definitie. Fiind data o
functie g(n), prin Q(g(n)) se desemneaza o
multime de functii definita
astfel:
Q(g(n)) [2.3.1.a]
- Se spune ca o functie f(n)
apartine multimii Q(g(n)), daca exista
constantele pozitive c1 si c2 ,
astfel incat ea poate fi "cuprinsa" (ca un 'sandwich') intre c1 g(n) si c2
g(n) pentru un n
suficient de mare.
Fig.2.3.a. Reprezentarea lui f(n) =
Q(g(n))
- Desi Q(g(n)) reprezinta o multime de
functii, se utilizeaza uzual notatia f(n) =
Q(g(n)), cu semnificatia "f(n) este Q(g(n)) ", indicand astfel faptul
ca f(n)
este membru al lui Q(g(n) sau
ca f(n) I Q(g(n)) [2.3.1.b]. f(n) =

Cu alte cuvinte pentru orice n > n0 , f(n) este egala cu g(n) in interiorul unui factor constant.
Se spune ca g(n)
este o margine asimptotica
stransa ('asymptotically tight bound') a lui f(n).
Definitia lui Q necesita ca fiecare membru a lui Q(g(n)) sa fie asimptotic pozitiv, deci f(n)
sa fie pozitiv pentru valori
suficient de mari ale lui n.
- In practica,
determinarea lui Q in cazul unei
expresii, se realizeaza de regula luand in considerare termenii
de ordinul cel mai mare si neglijand restul termenilor.
- Aceasta
afirmatie poate fi demonstrata
intuitiv, utilizand
definitia formala a lui Q in a arata ca
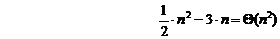
o
Pentru aceasta, constantele c1 , c2 si n0 trebuiesc determinate astfel incat,
pentru orice n n0 sa fie valabila relatia:

o
Se impart membrii inegalitatii cu n2 si se obtine

o
Inegalitatea din dreapta este valabila pentru orice n 1 daca il alegem pe c2 1/2.
o
Inegalitatea din stanga este valabila pentru orice
valoare a lui n 7
daca se alege c1 1/14 .
o
Astfel, alegand c1
= 1/14 , c2
= 1/2 si n0 = 7 se
poate verifica simplu ca



