Echilibrul producatorului. Analiza pe termen lung

Echilibrul producatorului. Analiza pe termen lung

Pe termen scurt firma trebuie sa aleaga cum sa-si utilizeze cel mai bine capacitatile de productie existente, utilajele si echipamentele in care deja a investit, pe termen lung ea trebuie sa decida in care din utilaje, echipamente si tehnologii de fabricatie trebuie sa investeasca.

Optiunile producatorului pe termen lung sunt decizii strategice si cu grad ridicat de risc. Pe termen lung, teoria producatorului se ocupa, asadar, de acele situatii in care capacitatile de productie si tehnologiile la care are acces firma fac obiectul schimbarii. In aceste situatii, insasi functia de productie se schimba astfel incat intrarile date de L si K sunt asociate cu cantitati diferite de productie sau invers, un anumit nivel al productiei poate fi asociat unor intrari diferite din cei doi factori de productie. Pentru a fi competitiva, firma trebuie sa aleaga din multitudinea alternativelor tehnice de combinare a factorilor pe cea care permite obtinerea celei mai mari productii la anumite intrari sau costuri cu cei doi factori de productie sau, analog, realizarea productiei dorite cu cele mai mici costuri posibile.

Folosind metodologia deja cunoscuta de la teoria consumatorului, in continuare, vom analiza alegerile pe termen lung ale producatorului si situatiile de echilibru ale acestuia. Presupunem ca munca (L) si capitalul (K) sunt factori perfect divizibili si adaptabili si, deci, substituibili. In acest caz, productivitatile lor marginale pot fi definite drept derivata partiala a functiei de productie in raport cu factorul considerat:

; 

Ilustrarea grafica a modurilor de combinare a intrarilor din cei doi factori pentru obtinerea unui volum dat de productie, se realizeaza cu ajutorul asa-numitelor izocuante sau curbe de izoprodus (curbe ale unor productii constante, egale - "izo" inseamna egal).

Izocuanta evidentiaza ansamblul combinatiilor factorilor de productie
care permit obtinerea aceluiasi volum de productie. Ea este dedusa din functia de productie cunoscuta (Q = Q(L,K)), prin modificarea lui L si K in asa fel incat Q sa fie mentinut constant.

Figura 5.2 prezinta o anumita izocuanta care arata seria de combinatii sau posibilitati tehnologice pentru a produce un nivel dat al productiei. Astfel, acelasi nivel al productiei (de exemplu turnarea a Q₁ = 100 m² de asfalt pe o sosea) poate fi realizat fie utilizand o cantitate mare de capital si mai putina forta de munca (combinatia a), fie folosind o cantitate mai mica de capital si mai multa forta de munca (combinatia d). Din moment ce curba este continua, sunt posibile o infinitate de metode sau combinatii de productie; ele sunt combinatii ale unor productii egale si se bazeaza pe substituirea factorilor de productie.

Rata marginala de substituire (RMS) reprezinta cantitatea dintr-un factor necesara pentru a compensa pierderea potentiala de productie determinata de reducerea intrarilor din celalalt factor de productie. RMS masoara, deci, rata la care un factor este substituit cu altul, pentru a mentine productia constanta:

Pe masura ce se trece de la un punct al izocuantei la altul, productia este mentinuta constanta prin substituirea unui factor cu altul. Raportul masoara rata de substitutie intre diferite puncte de pe izocuanta. Astfel, daca firma care asfalteaza soseaua doreste sa se deplaseze din punctul "b" in punctul "a" pentru a utiliza relativ mai mult capital (DK = 20 - 12) si mai putina forta de munca (DL = 8 - 4), ea poate mentine acelasi nivel al productiei (100 m²) substituind o unitate din factorul munca cu doua unitati din factorul capital ().

Rata marginala de substituire este evidentiata grafic prin valoarea pantei izocuantei intr-un anumit punct. RMS ia valori diferite pe tot parcursul izocuantei (care este o curba convexa la origine) si este egala, in orice punct al ei, cu raportul invers dintre productivitatile marginale ale celor doi factori in acel punct:

RMS= - dK/dL= Q'_K/Q'_L

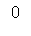
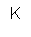
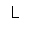Rata marginala de substituire ofera informatii utile privind combinarea si substituirea intre factori pentru un nivel de productie dat. Fiecarui nivel de productie ii corespunde o izocuanta, care reda combinatii alternative de factori care conduc la atingerea acelei productii. Daca pe un singur grafic reprezentam mai multe izocuante, obtinem o harta a izocuantelor.

Harta izocuantelor reprezinta ansamblul izocuantelor care ofera informatii producatorului asupra diferitelor niveluri de productie posibil de atins in diverse combinatii ale factorilor de productie. In Figura 5.3 este prezentata o harta cu patru izocuante, una pentru fiecare nivel de productie (Q₄ > Q₃ > Q₂ > Q₁). Generalizand, putem imagina in planul axelor L0K o infinitate de izocuante, fiecare corespunzand unui nivel dat al productiei. Cu cat sunt mai indepartate de origine, cu atat izocuantele releva niveluri mai ridicate de productie.

Posibilitatile de optiune ale producatorului se manifesta in conditiile unor restrictii (constrangeri) determinate de volumul resurselor sau al bugetului de care dispune (R) si de preturile factorilor de productie (P_L, P_K) care nu sunt sub controlul acestuia; ele sunt variabile exogene pentru decizia firmei.

Producatorul trebuie sa opteze atat asupra nivelului productiei, cat si asupra metodei (combinatiei) utilizate pentru a obtine acel volum al productiei. In momentul deciziei, producatorul dispune de un volum limitat al resurselor sale, pe care le va investi (cheltui) pentru achizitionarea celor doi factori, ceea ce inseamna ca:

Aceasta este ecuatia unei drepte cu panta negativa (), numita dreapta sau linia izocostului. Ea este analoaga dreptei bugetului de la teoria consumatorului.

Linia izocostului evidentiaza ansamblul combinatiilor posibile de factori de productie pe care producatorul poate sa-i achizitioneze cheltuind integral bugetul sau resursele sale disponibile.

Dupa cum se observa din Figura 5.4, orice punct al dreptei NS reprezinta o cheltuiala egala ca marime, dar cu o repartizare diferita intre L si K, punctele extreme fiind: punctul N de intersectie al dreptei cu axa ordonata, cand intregul buget este investit in capital () si punctul S de intersectie al dreptei izocostului cu abcisa, cand tot bugetul este cheltuit pentru achizitionarea factorului munca ().

Asadar, domeniul de optiune al producatorului este reprezentat de triunghiul ONS, inclusiv frontiera NS. Producatorul (firma) va tinde, tinand seama de constrangerea bugetara, sa produca cat mai mult posibil, sa maximizeze productia la un cost dat. Situatia de echilibru este obtinuta atunci cand firma nu mai poate sa-si mareasca productia in conditiile constrangerilor precizate.

In reprezentare grafica, echilibrul producatorului poate fi definit pornind de la confruntarea liniei izocostului cu harta izocuantelor. Linia izocostului are panta negativa si va fi intotdeauna tangenta uneia dintre izocuante. Dupa cum se vede si in Figura 5.5, echilibrul producatorului este atins in punctul E in care linia izocostului este tangenta la una din izocuante (in exemplul nostru, Q₂). Situarea acestui punct in grafic defineste atat nivelul maxim al productiei posibil de realizat (Q₂ = 200 m²), cat si combinatia de factori utilizati, reprezentata prin coordonatele L_E si K_E.

Pe baza aceleiasi metodologii de analiza, putem defini echilibrul producatorului pornind de la ipoteza in care acesta este pus in situatia sa minimeze costul pentru un nivel dat al productiei (in exemplul luat cu firma care executa lucrari de asfaltare, presupunem ca aceasta doreste sa realizeze o suprafata de 200 m²).

Potrivit acestei ipoteze, producatorul trebuie sa aleaga acea combinatie de factori (L si K) ale caror preturi sunt date (P_L si P_K) care sa-i permita realizarea nivelului dat de productie (Q_D) cu un cost (C = L·P_L + K·P_K) minim; in aceasta ipoteza, costul este, deci, variabila a carei marime trebuie minimizata prin metoda de productie utilizata.

In Figura 5.6 sunt reprezentate grafic mai multe drepte ale izocostului, fiecare corespunzand unor niveluri diferite (C₄ > C₃ > C₂ > C₁). Echilibrul firmei este atins in punctul (E) in care izocuanta corespunzatoare nivelului de productie determinat (Q_D) este tangenta la una din liniile izocostului (C₃). Acest punct (E) defineste nivelul minim al costului (C₃) cu care firma poate obtine volumul dorit de productie (Q_D = 200 m²) prin combinatia de factori utilizati (L_E si K_E). Acelasi volum de productie mai poate fi obtinut si prin alte metode sau combinatii de factori (de exemplu, R si T), dar care corespund unui cost mai ridicat (C₄).

In concluzie, pe termen lung, situatia de echilibru a producatorului presupune alegerea acelei combinatii de factori utilizati pentru a produce o cantitate data dintr-un bun cu cele mai mici costuri sau, ceea ce este acelati lucru, pentru a produce cea mai mare cantitate dintr-un bun la un cost dat. Ambele situatii - maximizarea productiei sub constrangerea bugetara (reprezentata grafic in Figura 5.5) si respectiv, minimizarea costului pentru o productie data (Figura 5.6) sunt similare (matematic se spune ca una este dualul celeilalte) si satisfac aceiasi conditie de echilibru: dupa cum se observa din ambele reprezentari grafice, pozitia de echilibru se afla in punctul unde panta izocuantei relevante are aceiasi valoare cu panta liniei izocostului.

Intrucat panta izocuantei este data de raportul productivitatilor marginale ale celor doi factori, care este egala cu rata marginala de substituire a lor in acel punct (), iar panta liniei izocostului este data de raportul preturilor celor doi factori (), putem formula conditia de echilibru a producatorului:

sau

Pentru a atinge pozitia de echilibru, producatorul trebuie sa puna in ecuatie raportul preturilor factorilor de productie (care nu se afla sub controlul sau ci este dat de preturile de pe piata) cu raportul productivitatilor marginale ale factorilor,care se afla sub controlul sau si deci il poate modifica prin ajustarea intrarilor din factorii respectivi. Astfel spus, producatorul sau firma aplica asa-numita regula a celor mai mici costuri.

Regula celor mai mici costuri consta in aceea ca, pentru a-si maximiza profitabilitatea, firma va ajusta intrarile din toti factorii de productie astfel incat productivitatea marginala a fiecarei unitati monetare cheltuite cu fiecare factor de productie are acelasi nivel. Ea este similara cu legea egalizarii utilitatii marginale pe unitatea monetara cheltuita de consumator (analizata in Capitolul 4) si are la baza o alta regula (intalnita si la teoria consumatorului) si anume, regula sau principiul substitutiei.

Principiul substitutiei opereaza atunci cand intervin modificari in raportul dintre preturile factorilor de productie (panta liniei izocostului se modifica), fapt care il determina pe producator sa inlocuiasca partial factorul de productie care a devenit relativ mai scump cu cel care a devenit relativ mai ieftin.

Regula sau principiul substitutiei intervine de fiecare data cand cei doi termeni ai ecuatiei ce definesc conditia de echilibru a producatorului nu mai sunt egali. Astfel, daca raportul este mai mare decat raportul (sau ), atunci firma, aplicand regula celor mai mici costuri, va substitui capitalul prin munca pana va restabili echivalenta productivitatilor marginale dobandite pe unitatea monetara cheltuita. Dimpotriva, daca atunci firma isi poate ameliora profitabilitatea substituind forta de munca prin echipamente de productie sau capital devenit acum relativ mai ieftin.