Pitagora din Samos ( 580-490?500 i.Hr. )

Pitagora din Samos ( 580-490?500 i.Hr. )

Pitagora ( Pythagoras ) a fost un filosof si matematician grec, originar din insula Samos ( nu departe de Milet ), in nordul insulelor Sporade, intr-o familie instarita. Tatal, Mnesarchos, si mai ales mama, Partenisa, s-au ingrijit de educatia lui. Primul sau dascal care l-a initiat de altfel in filosofie a fost Hermodamos din Samos, apoi Pherekydes din Syros, iar la Milet a studiat cu Thales si Anaximandru. Thales era pe atunci destul de batran, insa cu siguranta l-a impresionat pe tanarul de 18 ani foarte mult. A facut calatorii in Egipt ( timp de 22 de ani ), in Babilon, in Chaldeea ( timp de 12 ani ), probabil ca si in India, de unde a luat invataturi. In jurul anului 540 i.Hr., Pitagora s-a intors in Samos, insa oranduielile politice din insula se schimbasera, aristocratia fusese infranta de catre demos si inlaturata de la putere, iar pe insula se instaurase regimul tiranului Polycrates. In jurul varstei de 40 de ani, Pitagora se autoexileaza la Crotona, in sudul Italiei. Se pare ca a fost si conducatorul partidului aristocratic din Crotona. Nu este exclusa posibilitatea ca Pitagora sa fi conspirat impotriva regimului lui Polycrates, iar acest fapt sa fi determinat exilarea sa atat de departe. La Crotona, figura lui Pitagora ramane tot asa de confuza si controversata, intre un profet - intemeietorul unei noi comunitati religioase, ganditor - liderul unei scoli filosofice care cultiva intens matematica si muzica, si lider politic si chiar conducatorul unei organizatii secrete. De aceea, se pare ca activitatea politica a pitagoricienilor nu era vazuta cu ochi buni de autoritati. In jurul anului 503 i.Hr., la Crotona izbucneste o rascoala impotriva pitagoricienilor, ceea ce justifica faptul ca erau deja destul de numerosi, puternici si influenti. Se pare ca in aceste imprejurari confuze Pitagora si-ar fi gasit moartea, in jurul varstei de 80 de ani. Asadar, in urma rascoalei, pitagoricienii au fost nevoiti sa se retraga din Crotona.

Pitagora a fost un mare educator si invatator al spiritului grecesc si se spune ca a fost si un atlet puternic, asa cum statea bine atunci poetilor, filosofilor si comandantilor militari.

Una dintre marile sale realizari a fost intemeierea la Crotona a unei scoli filosofice, care avea motto-ul: "Totul este numar". Scoala lui Pitagora avea si o emblema, si anume "Pentagonul stelat" sau "Pentagrama". Pentagrama isi face aparitia inca din cele mai vechi timpuri ( 3000 i.Hr. ), fiind intalnita in scrierile mesopotamiene ( scrieri pictografice precuneiforme ). Adeptii lui Pitagora foloseau acest simbol ca semn al recunoasterii. Ei numeau Pentagrama "Hugieia" ( Hugieia ═ zeita greaca a sanatatii ), care se traduce prin "Sanatate", insa are mai mult sensul de intregime, si mai general "orice binecuvantare divina". Adeptii lui Pitagora au marcat unghiurile Pentagramei cu literele grecesti UGIEIA. Literele erau asezate pe colturile Pentagramei, aranjate in sens invers acelor de ceasornic, incepand din coltul din stanga de jos.Geometria Pentagramei si aspectele sale metafizice au fost examinate de catre adeptii lui Pitagora. Se observa ca Pentagrama formeaza in centru, prin unirea liniilor, un pentagon. Colturile pentagonului unite, formeaza la randul lor un alt pentagon in interior, si asa mai departe Deci, putem conchide ca Pentagrama reprezinta si un simbol al infinitului.

Pentagrama lui Pitagora

Doctrina acestei scoli era bazata pe ideea ca matematica guverna universul. Ca si Democrit din Abdera, Pitagora credea despre univers ca este discret. Se pare ca Pitagora a folosit primul numele "mathematica" ( ═ "ceea ce se invata" ), pentru cunostintele de matematica.

Scoala lui Pitagora functiona ca o confuzie secreta, despre care povestesc scriitorii mai tarzii, ca Iamblichos ( "De vita pythagorica", tradusa in limba romana ), Aulus Gellius ( "Noptile attice" ), Plutarch ( care da Teoremei 47 din Cartea I a "Elementelor" lui Euclid, numele de "teorema lui Pitagora" ), Philolaus ( "Despre Pythagora si pythagorei" ). Iamblicos afirma in lucrarea sa "De vita pythagorica" ca filosofia pitagoricienilor era alcatuita din acusmate, precepte de ascultare, nedemonstrabile, care talcuiesc ce este, ce este mai presus si ce trebuie sa faci sau sa nu faci. Iata cateva exemple:

"Cel mai bun? Fericirea"

"Lucrul cel mai dificil? Cunoasterea de sine"

Ce sunt insulele Fericitilor? Soarele si Luna".

Potrivit unei legende se spune ca Pitagora, fiind intrebat de Policrate din Syracusa cati elevi are, a raspuns: jumatate studiaza matematica, un sfert muzica, a saptea parte asista in tacere, iar in plus mai sunt inca trei femei. Asadar, Pitagora avea 28 de elevi in scoala sa filosofica.

Aulus Gellius povesteste in Noptile attice" cum erau primiti adeptii: examinati dupa fizionomie, cei gasiti apti erau primiti la invatatura. Elevilor li se prescria un timp de tacere de minimum doi ani, in care ascultau fara sa intrebe ( erau akustikoi, auditori ), invatand lucrurile cele mai grele: tacerea si ascultarea. Deveneau apoi mathematici, studiind geometria, muzica si alte discipline superioare. Asadar, pitagoricienii cunosteau patru mathemata ( adica ceea ce trebuie invatat ), domenii ale stiintei: stiinta despre numere - Aritmetica, teoria muzicii - Armonia, stiinta despre figuri - Geometria si stiinta despre corpurile ceresti - Astrologia ( Astronomia ). "Figuri cosmice" erau numite de grecii antici poliedrele regulate, care erau cunoscute pe vremea lui Pitagora, si anume tetraedrul regulat, cubul ( hexaedrul regulat ) si dodecaedrul. Pentru Pitagora, era normal sa-ti placa mai mult geometria, stiinta filosofului prieten al egalitatii, stiinta poporului si a negustorului dornic de castig. Adeptii deveneau, in fine, fizicieni ( physikoi ). Pentru pitagoricieni, descoperirile individuale erau proprietatea scolii, descoperitorii ramanand in umbra.

Inca din antichitate, s-a facut o distinctie intre pitagoricieni, care erau discipolii directi ai lui Pitagora, pitagorei, elevi sau urmasi acelora si pitagoristi, cei care traiesc dupa primcipiile scolii, dar din afara.

Ca scoala de gandire filosofica, pitagoreismul a fost idealist si conservator.

Pitagora apare si in cateva despre epigramele pallatine:

"Tacerea-i o desavarsita invatare a noastra,

O marturie ne-a dat Pythagoras cel intelept,

Care, stiind sa vorbeasca, ne-nvata scoala tacerii,

Gasind pentru suflet un leac in stapanirea de sine

Pitagoricienii au fost mai ales aritmeticieni ( arithmos ═ numar, in limba greaca ). Am vazut din cele relatate anterior ca motto-ul scolii era: "Totul este numar". La vechii greci, numar inseamna de fapt numar natural. Pe langa proprietatile lor matematice, aceste numere au fost investite de pitagoricieni cu o mistica care a stat la baza organizarii vietii ca si a filosofiei acestora. Astfel, numarul 1 reprezinta simbolul ratiunii, generatorul tuturor numerelor, numarul 2 este primul numar par sau feminin, numarul opiniei sau al parerii, numarul 3 este numarul masculin, al armoniei, fiind compus din unitate ( 1 ) si diversitate ( 2 ), numarl 5 reprezinta simbolul casatoriei, adica reuniunea numarului feminin 2 si masculin 3, numarul 10 reprezinta universul ( tetraktis-ul ), adica suma primelor patru numere naturale.

Numarul pentru pitagoricieni reprezenta o colectie de unitati, deci puteau fi doar numere intregi pozitive. Unitatile care alcatuiesc numarul au fost considerate indivizibile si au fost reprezentate prin puncte, situate in felul unor figuri geometrice regulate.

Din studiul numerelor, pitagoricienii au conceput "numerele figurative", cum sunt numerele triunghiulare ( numere dispuse sub forma unui triunghi,adica: 1, 1 + 2 ═ 3, 1 + 2 + 3 ═ 6, reprezentarea lor generala fiind: 1 + 2 + 3 + + n ═ 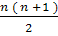), patratice ( numere dispuse sub forma unui patrat, adica: 1, 1 + 3 ═ 4, 1 + 3 + 5 ═ 9, reprezentarea lor generala fiind: 1 + 3 + 5 + + ( 2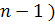 ═ 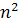),hexagonale ( numere dispuse sub forma unui hexagon, adica: 1, 6, 15, 28, 45, reprezentarea lor generala fiind: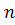 ( 2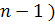), pentagonale ( numere dispuse sub forma unui pentagon, adica: 1, 1 + 4 ═ 5, 1 + 4 + 7 ═ 12, reprezentarea lor generala fiind: 1 + 4 + 7 + + ( 3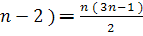 ), dreptunghiulare ( erau numere compuse ce se descompun in produs de doi factori, - "numere plane", reprezentate sub forma unui dreptunghi), tetraedrale ( numere dispuse sub forma unui tetraedru ), cubice ( numere dispuse sub forma unui cub, adica: 1, 1 + 3 ═ 4, 1 + 3 + 6 ═ 10, reprezentarea lor generala fiind: 1 + 3 + 6 + + 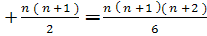), numere paralelipipedice ( erau numere compuse ce se descompuneau in produse de trei factori, - "numerele corporale", si erau reprezentate sub forma de paralelipipede ) numerele perfecte, numerele amiabile, numerele pare si impare, numerele liniare ( acele numere simple care nu se descompun in produs de factori ). Un exemplu concret de numere prietene sau amiabile ( numere prietene ═ acele numere in care fiecare numar este suma divizorilor celuilalt numar ) o reprezinta perechea ( 220, 284 ), care este de fapt singura pereche de acest gen cunoscuta in antichitate. Regula de formare a numerelor prietene a fost descoperita de matematicianul arab Tabit ibn Korra, uitata apoi si redescoperita ulterior de matematicianul francez Pierre Fermat in secolul XVII. Acesta descopera perechea ( 17 296, 18 416 ). La ora actuala se cunosc si alte perechi de numere prietene, ca de exemplu: ( 1184, 1210 ), ( 2620, 2924 ), ( 5020, 5564 ), ( 6232, 6368 ). Se spune ca Pitagora la intrebarea cine este prietenul a afirmat: Acela care este alt eu, ca numerele 220 si 284".

Cu ajutorul calculatorului electronic, intr-u universitate din SUA au fost cercetate toate numerele pana la un million. Dupa numerae cercetari s-a obtinut colectia a 42 de perechi de numere perfecte.S-au descoperit de asemenea si perechi de numere prietene impare, ca de exemplu: ( 12 285, 14 595 ), ( 67 095, 87 633 ), etc.

Prin numar perfect, pitagoricienii intelegeau acel numar pentru care suma divizorilor sai, notata prin S ( exceptand numarul insusi ) este egala cu numarul insusi N. Ca exemple de numere perfecte, pitagoricienii au descoperit urmatoarele numere: 6, 28, 496, 8128. Toate aceste numere perfecte sunt pare si sunt date prin formula general 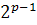( 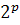- 1 ), unde 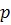si 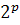- 1 sunt numere prime. La ora actuala nu se stie daca exista numere perfecte impare.

O semnificatie deosebita a avut-o in scoala pitagoreica numarul 36. Acest numar i-a impresionat pe pitagoreici datorita proprietatilor sale. Pe de o parte, el reprezinta suma cuburilor primelor trei numere natural ( 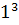+ + 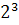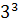), iar pe de alta parte, este suma primelor patru numere pare si impare: ( 2 + 4 + 6 + 8 ) + ( 1 + 3 + 5 + 7 ) ═ 36. Conform parerii potagoricienilor, intreg universul a fost construit pe primele patru numere pare si impare, de aceea cel mai groaznic juramant era considerat juramantul cu numarul 36.

Marele scandal al scolii pitagoreice l-a constituit descoperirea de catre ei a numerelor irationale. Aceasta descoperire contrazicea fundamental invataturii pitagoreice conform careia totul este numar" ( sau numerele naturale reprezinta masura tuturor lucrurilor ), in timp ce 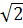nu era considerat numar. Descoperirea numerelor irationale constituie cea mai mare realizare a scolii pitagoreice in matematica.

In limba greaca, irationalitatea era exprimata prin doi termeni: asimmetron ═ care nu are masura comuna si alogon ═ inexprimabil prin logos, deci prin raportul a doua numere ( Platon foloseste termenul arreton ). Denumirea latina "irational" provine din traducerea ultimului termen alogon, caci ratio inseamna raport, iar prefixul "i" reprezinta negatia. Diferenta dintre denumirile asimmetron si alogon reflecta diferenta dintre cele doua moduri de a intelege irationalitatea, sub aspect "geometric", relativ ( perechi de segmente care nu au o masura comuna ), sau sub aspect "aritmetic", intrinsec ( numar inexprimabil ca si catul a doua numere naturale ). Este foarte probabil ca descoperirea irationalitatii numarului 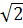este strans legata de "teorema lui Pitagora", din cauza ca diagonala unui patrat de latura 1 si latura sa sunt asimmetron, adica lungimea diagonalei prin raport cu latura este alogon. Nu este exclusa nici varianta conform careia, numarul 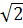sa fi fost obtinut de pitagoricieni in muzica ( teoria armoniei ) sau ca media proportionala 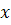a numerelor 1 si 2, astfel incat ═ . Potrivit unei legende, pitagoreicul Hippasos din Metapont ( oras in sudul Italiei ) a pierit intr-un naufragiu datorita faptului ca a divulgat descoperirea irationalitatii numarului 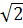in afara scolii, si de aceea a fost pedepsit de zei.

Pitagoreicii erau vegetarieni si credeau in reancarnare ( influente indice ).

Pentru Pitagora, dintre figurile solide, cea mai frumoasa este sfera, iar dintre cele plane, cercul, iar dintre numere, 10 este numarul perfect ( 1 + 2 + 3 + 4 ═ 10 ). Pentru adeptii scolii pitagoreice, 10 reprezinta universul, perfectiunea, tetraktis-ul. Tetraktis-ul a fost gandit ca numar ce cuprinde izvorul si radacina vesnic curgatoarei naturi". Pentru a justifica ca numarul 10 reprezinta perfectiunea, Pitagora a adaugat celor noua cercuri ( Cer, Soarele, Luna, Pamant, Mercur, Venus, Marte, Jupiter, Saturn ), cel de-al zecelea - al Anti-Pamantului ( o inventie arbitrara ).

Construirea poligoanelor si poliedrelor regulate i-a impresionat foarte mult pe cei care au gasit solutia, deoarece aceste figuri erau considerate figuri cosmice". Fiecarei figuri cosmice i se atribuia denumirea unei stihii, incluse dupa parerea grecilor, in bazele existentei: tetraedrul se chema foc, octoedrul - aer, icosaedrul - apa, dodecaedrul - univers, hexaedrul - pamant. Dintre toate corpurile geometrice, cea mai perfecta a fost considerata sfera. Asrfel, Pitagora a ajuns la concluzia ca Pamantul este sferic.

Pitagorismul admitea existenta a zece principii care germineaza cosmosul: finitul si infinitul, unul - pluritatea, repaus - miscare, lumina - intuneric. Cosmosul

( notiune introdusa de pitagoreici ) reprezinta armonie, tetraktis, perfectiune, ordine, masura. Masura a fost corelata de altfel cu " momentul potrivit" sau cu " potrivirea favorabila".

In geometrie, am observat ca "teorema lui Pitagora", desi atribuita de catre Plutarch, Diogene Laertius si Proclus, era cunoscuta pentru cazuri particulare in China antica, Babilonia, Egipt. Unii considera ca Pitagora a fost primul care a dat o demonstratie riguroasa a acestei teoreme, altii insa nu recunosc acest fapt.

In Franta si unele regiuni ale Germaniei, in evul mediu, teorema lui Pitgora se numea "puntea magarilor". La matematicienii Orientului, aceasta teorema era cunoscuta sub denumirea "teorema miresei". Istoria insa este urmatoarea: in unele texte, cum ar fi "Elementele" lui Euclid, aceasta teorema se numea "teorema nimfei", pentru asemanarea desenului cu o albina sau un fluture, ceea ce in limba greaca se numea "nimfa". La traducerea din limba greaca in limba araba nu s-a atras atentie la desen, astfel ca "nimfa" s-a transformat in "fluture" sau "mireasa".

Conform unei legende, aflam ca Pitagora dupa ce a demonstrat celebra teorema, a multumit zeii sacrificand 100 de boi ( hecatomb ). Aceasta legenda nu seamana adevarului, deoarece Pitagora era vegetarian si un adversar neampacat al sacrificarii animalelor.

Teorema lui Pitagora

Asadar, teorema lui Pitagora stabileste o relatie intre lungimile laturilor unui triunghi dreptunghic: suma patratelor lungimilor catetelor este egala cu patratul lungimii ipotenuzei.

Ilustrarea teoremei lui Pitagora

Subiectul acesta legat de teorema lui Pitagora poate fi impartit in trei: cunoasterea tripletelor pitagoreice ( 3, 4, 5 ), ( 5, 12, 13 ),( 12, 35, 37 )), cunoasterea teoremei propriu-zise si cunoasterea unei demonstratii.

Tripletele pitagoreice sunt cunoscute de foarte mult timp, ele fiind folosite la construirea unui unghi drept in conditii practice: o sfoara este marcata cu noduri aflate la anumite distante; formand din ea un triunghi, triunghiul format este dreptunghic. Metoda poate fi folosita de exemplu pentru montarea in pozitie verticala a unui catarg de vas.

Prin triplet pitagoreic, intelegem un triplet de numere naturale nenule de forma (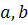 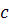) cu max ( 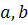) < 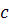care verifica conditia + ═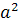

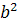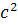
Abia dupa ce oamenii au invatat sa scrie, sa citeasca, iar calculul numeric a devenit o indeletnicire obisnuita, in sensul ca se puteau efectua cele 4 operatii si se cunostea ridicarea unui numar la patrat, ori extragerea radacinii patrate , s-a constatat ca cele trei lungimi, care stabilesc forma triunghiului dreptunghic, sunt asa incat patratul construit pe ipotenuza are aceeasi suprafata ca si suma ariilor celor doua patrate construite pe laturile unghiului drept. Cu alte cuvinte, se putea scrie relatia 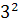+ 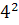═ 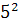. In zilele noastre spunem ca aceasta relatie exprima "teorema lui Pitagora". Pe vremea aceea insa, Pitagora nu se nascuse inca. Teorema care-i va purta numele a fost cunoscuta cu mult timp inaintea lui. In acele vremuri acest triunghi era considerat sacru, iar geometrii isi puneau intrebarea daca nu cumva mai sunt si astfel de triunghiuri sacre. Raspunsul la aceasta intrebare a fost bineinteles afirmativ.

Intr-unul din textele cuneiforme, descoperite in campia Mesopotamiei, vechi de aproape 5000 de ani, dar descifrat in secolul nostru, s-au gasit laturile a 15 triunghiuri dreptunghice exprimate cu numere intregi, ca de exemplu:

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

+ ═

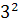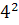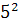
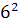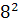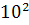
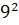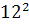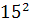
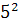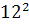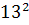
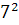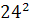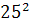
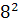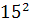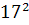
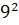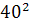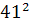
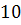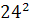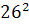
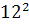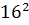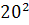
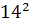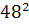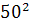
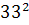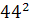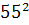
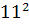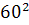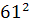
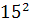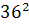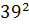
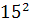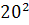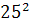
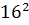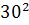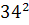
Aceste rezultate gasite pe tablitele de argila arsa ale sumerienilor si ale babilonienilor arata ca, acum 7 sau 8 milenii traiau pe campia Mesopotamiei niste calculatori ingeniosi, care descoperisera diverse metode algebrice pe care le utilizau in rezolvarea de probleme. Pornind de la relatia corespunzatoare triunghiului cu laturile 3, 4, 5 si inmultind toti termenii ei cu 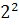, se obtine relatia

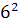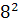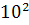+ ═ , adica triunghiul dreptunghic avand laturile 6, 8, 10.

Tot pe atunci triunghiul dreptunghic a fost bine-cunoscut si de catre hindusi,caci atat ritualul ceremoniilor religioase, care prescria o anumita pozitie a altarului, cat si problemele de constructii arhitectonice impuneau folosirea lui. De asemenea, stim ca hindusii aveau relatii comerciale si culturale cu babilonienii inca din mileniul al III-lea i.e.n. Intr-unul dintre cele mai vechi manuscrise, intitulat "Regulile funiei" ( Sulva sutra ), regasim "teorema lui Pitagora" exprimata astfel: "Daca pe diagonala unui dreptunghi se construieste un patrat, el este la fel de mare cu ceea ce rezulta daca se construiesc separat patratele pe lungimea si latimea lui". Tot in acest manuscris sunt prezentate reguli de costruire a unghiului drept cu ajutorul funiei cu noduri.

Monumente megalitice de acum 6000 de ani ( in Egipt ) sau 4500 de ani ( in insulele Britanice ) contin triunghiuri dreptunghice cu laturi de lungimi numere intregi, insa aceasta nu inseamna ca cei care le-au construit au stiut acest lucru. De asemenea, scrieri vechi din Regatul Mijlociu Egiptean si din Mesopotamia mentioneaza triplete pitagoreice.

"Sulva Sutra" lui Baudhayana, scrisa in sec. 8 i.Hr. in India, contine o lista de triplete pitagoreice descoperite algebric, un enunt al teoremei, precum si o demonstratie pentru un triunghi dreptunghic isoscel.

"Sulva Sutra" lui Apastamba ( cca. 600 i.Hr. ) contine o demonstratie numerica a cazului general, pe baza de arii. Unii cercetatori sustin faptul ca Pitagora s-ar fi putut inspira de la indieni in ceea ce priveste demonstrarea teoremei.

In jurul anului 400 i.Hr., conform lui Proclus, Platon a dat o metoda pentru determinarea tripletelor pitagoreice, metoda care combina algebra cu geometria.

Exista asadar o infinitate de triplete pitagoreice, forma lor generala fiind:

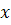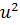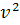═ - , y ═ 2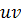, z ═ 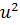+ 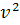, unde 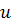si 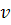sunt numere naturale oarecare, prime intre ele, adica (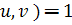, si > .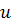

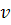Dupa aproximativ 100 de ani, Euclid a dat in cadrul lucrarii "Elemente" prima demonstratie axiomatica a teoremei.

Textul chinezesc "Chou Pei suan Ching" scris in perioada 500 i.Hr. - 200 d. Hr. contine o demonstratie vizuala a teoremei.

La ora actuala se cunosc aproximativ 400 de demonstratii ale teoremei lui Pitagora.

Exista numeroase metode de a demonstra celebra teorema, si anume:

Demonstratia data de Euclid in cartea I, teorema 47 din "Elemente", bazata pe echivalenta de arii;

Demonstratia data de Bhaskara Aciarya in cartea lui Ciu - Pei - Suan;

Demonstratie utilizand metoda vectoriala;

Demonstratia data de Leonardo da Vinci ( 1452 - 1519 ).

In ceea ce urmeaza vom ilustra o demonstratie a teoremei lui Pitagora.

Suprafetele ambelor patrate mari sunt egale cu 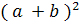. Daca suprafetele patratelor colorate cu roz, ce reprezinta patratele numerelor 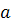si 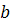( figura din stanga ) sunt substituite cu un patrat ce reprezinta numarul 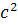, facandu-se simultan o rearanjare a jumatatilor celor doua dreptunghiuri (fiecare fiind format initial din cate doua triunghiuri dreptunghice, congruente cu cel initial ), se obtine figura reprezentata in partea din dreapta. Suprafetele celor doua patrate mari sunt identice, deoarece laturile acestora sunt congruente.

Calculand in fiecare caz suprafetele celor doua patrate, obtinem:

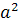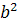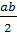S ═ + + 4 ( pentru patratul din stanga )

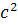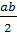S ═ + 4 ( pentru patratul din dreapta )

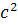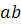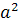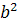Dupa un calcul relativ simplu se aunge la relatia + 2 ═ + + 2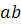, ceea ce conduce la relatia din teorema.

Demonstratie vizuala a teoremei lui Pitagora

In trigonometrie, relatia dintre sinusul unui unghi si cosinusul aceluiasi unghi este numita identitatea lui Pitagora, data prin relatia: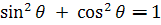

Ca o sinteza a realizarilor sale, amintim:

Numerele figurative si reprezentarea acestora;

nr. triunghiulare nr. patratice nr. pentagonale

Numerele prietene, perfecte, supraperfecte, imperfecte, pare si impare, irationale, etc.;

Proportiile de baza: media aritmetica, media geometrica ( proportionala ), media armonica si relatiile dintre ele:

═ ═ ═

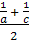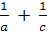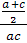Seria naturala a armonicelor ( exprimarea numerelor cu numere: unison, octava, cvinta, cvarta, terta majora, terta minora, sexta majora );

Teorema lui Pitagora;

Constructia pentagonului si decagonului regulat inscrise in cerc ( se utlizeaza impartirea razei AB in raportul , astfel ca 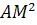═ AB . MB. Daca AB ═ r, AM ═ 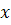, MB ═ 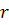- 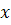, atunci se obtine ecuatia algebrica de gradul al II-lea in nedeterminata 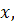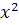+ 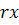- 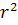═ 0 si ═ ).

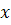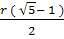Tipuri de proportii, listate in "Elementele" lui Euclid, prezentate in ceea ce urmeaza cu exemple numerice ( , ):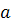

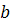
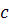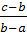═ ( media aritmetica ), ( 1, 2, 3 );

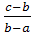═ ( media proportionala ), ( 1, 2, 4 );

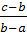═ ( media armonica ), ( 2, 3, 6 );

═ ═

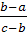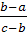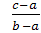═ , ( 6, 8, 9 );

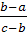═ , ( 3, 5, 6 ); ═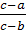

═ ═

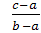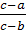Manuscrisele lui Pitagora - lasate fiicei sale, Demo, cu interdictia de a le pastra in secret - nu au fost cunoscute la timp de posteritate, de aceea este dificil sa i se delimiteze conceptiile si contributiile de ale discipolilor sai, iar prima descriere a operei si scolii sale a fost facuta, mult mai tarziu, de catre Philolaus.

"Prietenul care ne ascunde defectele ne slujeste mai rau decat dusmanul care ni le reproseaza" ( Pitagora ).