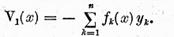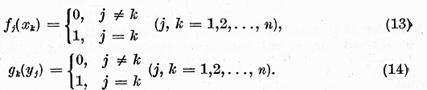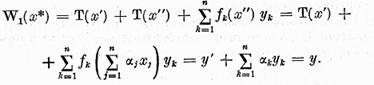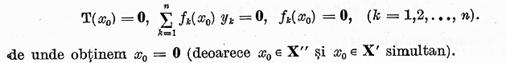Conditii necesare si suficiente pentru alternativa Fredholm pentru operatorul T

Conditii necesare si suficiente pentru alternativa Fredholm pentru operatorul T

Sa consideram ecuatia

si adjuncta ei

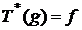(2)

Vom considera de asemenea ecuatiile omogene corespunzatoare

Amintim ca valabilitatea alternativei Fredholm pentru operatorul T inseamna ca :

fie ecuatiile (1) si (2) au solutii pentru orice membru drept si atunci solutiile lor sunt unice

fie ecuatiile omogene (3) si (4) au acelasi numar infinit de solutii liniar independente 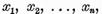respectiv 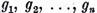, in acest caz pentru ca ecuatia (1) respectiv ecuatia (2) sa aiba solutie , este necesar si suficient ca

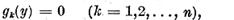
respectiv ca

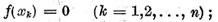
In plus solutia generala a ecuatiei (1) este data de egalitatea

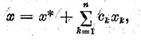
iar solutia generala a ecuatiei (2) de

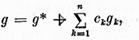
unde 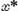(respectiv 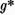) este o solutie oarecare a ecuatiei (1) iar 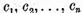sunt constante arbitrare

Teorema urmatoare arata ca clasa operatorilor T pentru care are loc alternativa Fredholm se deosebeste in esenta putin de clasa operatorilor de forma T = I - U , unde U este operator compact.

Teorema IV.1.1. Fiecare din urmatoarele doua conditii este necesara si suficienta pentru ca alternativa Fredholm sa aiba loc pentru operatorul T.

1. Operatorul T poate fi reprezentat sub forma

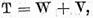
unde operatorul W are invers bilateral continuu, iar operatorul V este compact.

2. Operatorul T poate fi reprezentat sub forma

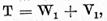
unde operatorul 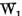are invers bilateral continuu, iar operatorul 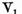este finit dimensional.

Demonstratie. Evident ne putem margini la demonstrarea suficientei conditiei 1) si necesitatii conditiei 2)

Suficienta conditiei 1) Fie

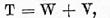
unde W are invers bilateral continuu, iar V este compact. Ecuatia (1) este echivalenta in acest caz cu ecuatia

Mai departe exista operatorul invers bilateral 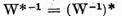de aceea ecuatia (2) este echivalenta cu ecuatia

in sensul ca daca 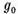este o solutie a ecuatiei(6) atunci 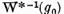va fi solutie a ecuatiei (2) iar daca 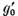va fi solutia ecuatiei (2) atunci 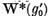va fi solutia ecuatiei (6)

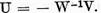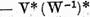
Sa introducem notatia Tinand cont de faptul ca 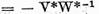putem reprezenta ecuatiile (5) si (6) sub forma

Deoarece operatorul U este compact pentru ecuatiile (7) si (8) este valabila concluzia teoremei I.4.1. Prin urmare ecuatiile omogene

au acelasi numar(finit) de solutii liniar independente 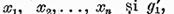Ecuatia omogena (3) va avea evident acelasi sistem complet de solutii liniar independente ca si ecuatia (9) anume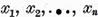. Sa demonstram ca functionalele

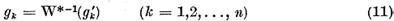
formeaza un sistem complet de solutii liniar independente ale ecuatiei(4). Faptul ca fiecare din functionale(11) este solutia ecuatiei (4) rezulta din echivalenta ecuatiilor (2) si (6) mentionate mai sus. Functionalele (11) sunt liniar independente deoarece relatia

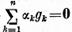
rezulta

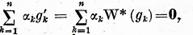
ceea ce este posibil doar daca In sfarsit daca ecuatia (4) ar avea o solutie 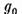care sa nu fie combinatie liniara de functionale (11) atunci functionala 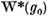ar fi o solutie a ecuatiei (10) care ar fi o conbinatie liniara de functionale 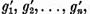ceea ce nu ar fi posibil.

Astfel ecuatiile (3) si (4) au acelasi numar finit de solutii liniar independente . Apoi pe baza teoremei I.4.1. ecuatia (5) si prin urmare si ecuatia (1) are solutie atunci si numai atunci cand

Aceasta conditie este echivalenta , in virtutea definitiei (11)

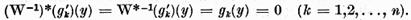
Analog se verifica faptul ca pentru solubilitatea ecuatiei (2) conditiile

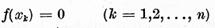
sunt necesare si suficiente.

Necesitatea conditiei 2). Fie 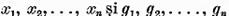sisteme complete de solutii liniare independente ale ecuatiilor (3) si (4). Atunci exista functionalele 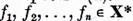si elementele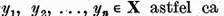

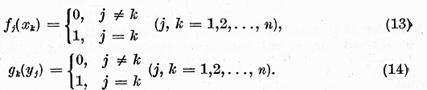
Sa notam 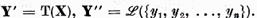Fiecare element 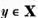poate fi reprezentat unic sub forma

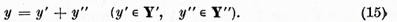
Intradevar daca punem

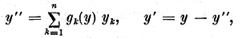
atunci in virtutea relatiei (14)

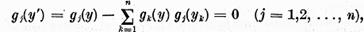
deci ecuatia 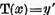are solutie si prin urmare 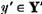. Unicitatea reprezentarii (15) rezulta din faptul ca daca

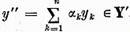
atunci ecuatia 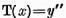trebuie sa aiba solutie si de aceea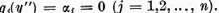

Sa notam acum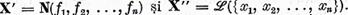

Se demonstreaza analog ca fiecare element 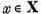poate fi reprezentat in mod unic sub forma

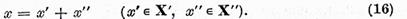
Vom construi operatorul W punand

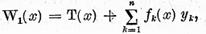
si vom demonstra ca W realizeaza o aplicatie bijectiva a spatiului X pe el insusi si prin urmare are un invers bilateral continuu

Pentru aceasta fie y un element arbitrar din X, 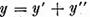reprezentarea lui sub forma (15). Aici

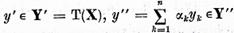
adica ecuatia 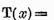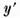are o solutie 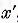care poate fi considerata a fi un element din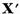

Punand

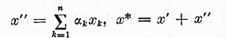
si tinand cont ca 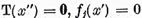si totodata de relatia (13) obtinem

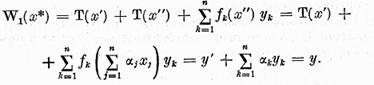
Sa aratam ca in afara de elementul x nu exista alte solutii ale ecuatiei 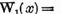y. Intradevar in caz contrar ar exista un element 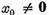astfel ca

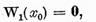
adica

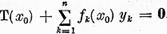
Aici 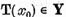iar

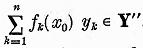
In virtutea unicitatii reprezentarii unui element sub forma (15) ajungem la relatiile

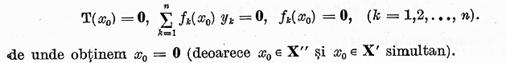
Pentru a incheia demonstratia teoremei este suficient sa definim