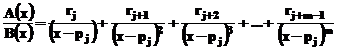Utilizarea operatorilor relationali
Mediul de programare MATLAB
utilizeaza, pentru compararea a doua matrici cu dimensiuni
identice, "element cu element", sase operatori relationali:
|
Operatori relationali
|
Semnificatia
|
|
<
|
Mai mic decat .
|
|
<=
|
Mai mic sau egal cu .
|
|
>
|
Mai mare decat .
|
|
>=
|
Mai mare sau egal cu .
|
|
Identic cu .
|
|
Diferit de .
|
Dupa
executarea operatiei, MATLAB afiseaza o matrice, identica
dimensional cu cele comparate, avand ca elemente "simbolurile" 1(unu) respectiv
0(zero), dupa cum relatia dintre elementele comparate este "adevarata" (TRUE) respectiv "falsa" (FALSE). Forma
generala a sintaxei este:
Rezultat=expresie_1 operator relational expresie_2
In care :
-Rezultat- este o matrice cu elementele 0 si 1,
obtinuta prin compararea celor doua expresii;
matricele sau
expresiile matriceale care se compara ;
|
|
-expresie_1
-expresie_2-
-operator relational- operatorii
relationali definiti in tabelul anterior.
Ex. :
Sa se compare elementele matricei 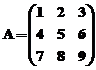 cu scalarul
cu scalarul 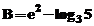 .
.
Folosind secvanta Matlab :
» A=[1,2,3;4,5,6;7,8,9]; B=exp(2)-log(5)/log(3);
» A<=B
ans =
1 1 1
1 1 0
0 0 0
» A>=B
ans =
0 0 0
0 0 1
1 1 1
» A==B
ans =
0 0 0
0 0 0
0 0 0
» A~=B
ans =
1 1 1
1 1 1
1 1 1
Ex. :
Sa se compare matricele 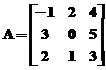 si
si 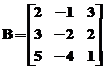 .
.
Cu
secventa MATLAB:
»
A=[-1,2,4;3,0,5;2,1,3];B=[2,-1,3;3,-2,2;5,-4,1];
se obtin rezultatele:
» A<B
ans =
1 0 0
0 0 0
1 0 0
»
A<=B
ans =
1 0 0
1 0 0
1 0 0
» A>B
ans =
0 1 1
0 1 1
0 1 1
» A>=B
ans =
0 1 1
1 1 1
0 1 1
» A==B
ans =
0 0 0
1 0 0
0 0 0
» A~=B
ans =
1 1 1
0 1 1
1 1 1
Operatori logici
MATLAB
utilizeaza trei operatori logici principali si unul auxiliar:
|
Operatori logici
|
Simbolizare
|
Semnificatie
|
Prioritate
|
|
NU
|
|
NOT
|
|
|
SI
|
&
|
AND
|
|
|
SAU
|
|
OR
|
|
|
SAU, exclus SI
|
|
XOR
|
|
Acesti operatori
lucreaza ca si cei relationali, element cu element, dar numai cu
matrici sau tablouri avand elemente logice: 0 sau 1. Daca
elementele unei matrici sunt zero si 1 sau valori diferite de zero, atunci cele diferite de zero se
seteaza, automat, la valoarea logica 1.
Obs: Operatorii logici nu
pot fi folositi in combinarea a doua expresii simbolice ("syms").
Precedenta operatorilor
Precedenta
operatorilor determina ordinea in care MATLAB realizeaza evaluarea
expresiilor. Ordinea in care sunt executate operatiile si prioritatea
operatorilor, in MATLAB, este caracterizata de urmatoarele nivele,
ordonate dinspre nivelul superior spre nivelul inferior:
Parantezele ( )
Transpunerea (.'),
puterea (.^), transpunerea conjugata complexa ('),
puterea matricilor (^);
Adunarea unara
(+), scaderea unara (-), negarea logica (~);
Inmultirea (.*),
impartirea la dreapta (./), impartirea la stanga (.),
inmultirea matricilor (*), impartirea la dreapta a
matricilor (./), impartirea la stanga a matricilor (.);
Adunarea (+),
scaderea (-);
Operatorul columnar
(:);
Operatorii
relationali: mai mic decat (<), mai mic sau egal decat (<=),
mai mare decat (>),mai mare sau egal decat (>=), egal cu (==),
diferit de (~=);
Operatorul logic SI
(&);
Operatorul logic SAU
(|);
Prioritatea
maxima o are operatorul NU,
ceilalti operatori logici avand prioritate egala, executia
acestora fiind data de regula "de la stanga la dreapta".
Prioritatea "de la stanga la dreapta" genereaza echivalenta intre
doua expresii relationale. Astfel, expresia a|b&c este echivalenta cu (a|b)&c. Oricum, in cele mai multe dintre limbaje, expresia a|b&c
este echivalenta cu a|(b&c), ceea
ce denota, de altfel, prioritatea operatorului & fata de |.
Pentru a exista compatibilitatea cu viitoarele versiuni MATLAB este indicat ca
utilizatorul sa foloseasca paranteze pentru a se specifica prioritatea de
executie a operatorilor & respectiv |. Urmatoarele doua expresii
ilustreaza prioritatea operatorilor:
1 | 0 & 0 = 0
0 & 0 | 1 = 1
Tabelul
de adevar al acestor operatori este:
|
Date de intrare
|
and
|
Or
|
xor
|
not
|
|
A
|
B
|
A&B
|
A|B
|
xor(A,B)
|
~A
|
~B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CUVINTE CHEIE
MATLAB rezerva o lista de
cuvinte cheie, lista care poate fi afisata, pentru evitarea
erorilor de evaluare si de redactare a expresiilor logice, cu functia
iskeyword, in linia de comanda MATLAB:
» [Cuvinte_cheie]=iskeyword
Cuvinte_cheie
=
'break'
'case'
'catch'
'continue'
'else'
'elseif'
'end'
'for'
'function'
'global'
'if'
'otherwise'
'persistent'
'return'
'switch'
'try'
'while'
Instructiunile "if ", "else elseif
Instructiunea "if"
("daca") poate fi
implementata in "format" simplu sau in asociere cu clauzele "else" ("altfel")
respectiv "elseif" ("altfel .
daca"). Actiunea instructiunii "if" trebuie sa se
finalizeze, intotdeauna, cu instructiunea "end" ("sfarsit"). Forma generala a
sintaxei este:
a) if expresie_logica
grup_de_instructiuni
end
b) if expresie_logica_1
grup_de_instructiuni_A
else
grup_de_instructiuni_B
end
c) if expresie_logica_1
grup_de_instructiuni_A
elseif expresie_logica_2
grup_de_instructiuni_B
end
d) if expresie_logica_1
grup_de_instructiuni_A
elseif expresie_logica_2
grup_de_instructiuni_B
else
grup_de_instructiuni_C
end
Diferenta dintre else si
elseif
se poate vedea in exemplul
urmator :
Instructiunea if- else Instructiunea if-
elseif
if A if A
x = a x = a
else elseif B
if B x = b
x = b elseif C
else x
= c
if C else
x = c x = d
else end
x = d
end
end
end
Ex.: Sa se calculeze valoarea expresiei :
 , pentru valorile intregi ale variabilei x.
, pentru valorile intregi ale variabilei x.
Se va folosi urmatoarea secventa
MATLAB (pentru simplificare se va utiliza functia length(x)
si o bucla repetitiva for, care va fi prezentata in
sectiunea urmatoare):
» x=-6:15;
» for k=1:length(x)
if
x(k)<-4
f(k)=exp(x(k)-3)-4
elseif
(x(k)>=-4)&(x(k)<=10)
f(k)=(log(x(k)^2+(2+sqrt(x(k)^4+3))^(1/3)))
else
f(k)=det([pi,3^(1/5);0.456,exp(x(k)^2-4)])
end
end
Rezultatul afisat de MATLAB este urmatorul :
f =
1.0e+096 *
Columns 1 through 7
-0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
sau, afisat in format rational :
f =
Columns 1 through 6
-32411/8103 -11923/2981 6083/2080 2719/1124 1804/1021 655/689
* * * *
Instructiunea de ciclare « for
Sintaxa pentru forma
generala este:
for index=expresie
grup_de_instructiuni
end
in care :
index -reprezinta contorul de iterare
expresie-
este o matrice, un scalar sau, de cele mai multe ori, o expresie de
forma :
n= »valoare initiala « : « pas » : « valoare finala »
Regulile specifice buclei « for » sunt:
-daca expresia atribuita indexului este un
scalar, bucla se executa o singura data, valoarea indexului
fiind valoarea scalarului
-daca expresia indexului este un vector linie,
bucla se executa de « n »
ori, unde « n » reprezinta
dimensiunea vectorului ;
-daca expresia este o matrice, indexul va
« lua » toate valorile matricei « pe coloana » ;
-daca expresia este de forma : »valoare initiala « :
« pas » : « valoare finala », iar pasul
are valoare pozitiva, atunci valoarea initiala trebuie sa fie
mai mica decat valoarea finala ;
-daca expresia este de forma : »valoare
initiala « : « pas » : « valoare
finala », iar pasul are valoare negativa, atunci valoarea
initiala trebuie sa fie mai mare decat valoarea finala ;
-daca expresia este de forma : »valoare
initiala « : « valoare finala », atunci
pasul de indexare este, implicit, 1 (unu).
Un
exemplu foarte simplu pentru utilitatea instructiunii de ciclare for,
ar fi calculul factorialului unui numar natural. Daca se cere
calculul numarului de permutari (factorialul), aferente lui n=10, se foloseste urmatoarea
secventa de instructiuni:
n = 10;
fact = 1;
for k = 1:n
fact = k * fact;
disp( [k fact] )
end
% FINAL PROGRAM
Rezultatul
afisat in fereastra de comanda, la apasarea tastei ENTER, este:
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
Multe
probleme in inginerie presupun dezvoltarea unui model matematic pentru
caracterizarea unui proces, in care variabila principala este
actualizata ciclic de-a lungul unei perioade de timp. Aceasta
operatie se numeste actualizare.
Pentru a exemplifica, se considera un proces de actualizare a temperaturii
unui corp, a carui temperatura initiala este 25 oC,
amplasat intr-un mediu a carui temperatura este 10 oC,
dupa un interval de mentinere la temperatura mediului, de 100 minute. Modul de abordare a
acestui tip de probleme este o cale standard:
se divide intervalul de timp in sub-intervale
egale (pasi), de lungime dt;
daca temperatura de start este Ti,
atunci se va folosi urmatorul model matematic, pentru calculul
temperaturii la un moment i+1, Ti+1:

in care, K este
un coeficient (valoarea K=0,05) care tine seama de imperfectiunile
mediului, iar Tf este
temperatura finala (Tf=10 oC). Fisierul script
realizat pentru rezolvarea problemei de actualizare,
stabileste valoarea initiala a intervalului de timp (a=0),
respectiv finala (b=100 minute). Daca intervalul de afisare nu
este un multiplu de pasul de calcul,
se va afisa un mesaj de eroare "Intervalul
de afisare nu este un multiplu de dt !":
K = 0.05;
Tf = 10; %temperatura finala
a = 0; % momentul initial
b = 100; % intervalul de timp
Timp_initial = a; % initializarea
intervalului de timp
T = 25; % initializarea temperaturii
dt = input( 'dt: ' ); % intervalul de calcul (pasul)
Intervalul_de_afisare = input('Afisarea rezultatelor la interval de
(minute):' );
if
Intervalul_de_afisare/dt ~= fix(Intervalul_de_afisare/dt)
disp( 'Intervalul de afisare nu este
un multiplu de dt !' );
end
format bank
disp( ' Timp Temperatura' );
disp( [Timp_initial T] ) % afiseaza momentul actualizarii si temperatura
for Timp_actualizare =
a+dt : dt : b
T = T - K * dt * (T -
Tf);
if
abs(rem(Timp_actualizare, Intervalul_de_afisare)) < 1e-6
disp( [Timp_actualizare T] )
end
end
%FINAL PROGRAM
Dupa
ultima linie de instructiuni, end,
(la apasarea tastei ENTER), se afiseaza, in linia de
comanda un mesaj prin care se cere utilizatorului sa introduca
pasul dt, apoi se cere stabilirea intervalului de afisare a
rezultatelor, dupa un interval de timp: "Afisarea rezultatelor la interval de (minute):". Pentru
exemplificare, se va rula, acest fisier, in doua variante (dt=0.2
si Intervalul_de_afisare=5, respectiv dt=0.3 si Intervalul_de_afisare=1.33),
rezultatele fiind:
Varianta I (dt=0.2
si Intervalul_de_afisare=5 )
dt: .2
Afisarea
rezultatelor la interval de (minute): 5
Timp Temperatura
0 25.00
5.00 21.67
10.00 19.08
15.00 17.06
20.00 15.49
25.00 14.27
30.00 13.32
35.00 12.58
40.00 12.01
45.00 11.56
50.00 11.22
55.00 10.95
60.00 10.74
65.00 10.57
70.00 10.45
75.00 10.35
80.00 10.27
85.00 10.21
90.00 10.16
95.00 10.13
100.00 10.10
Varianta II (dt=0.3
si Intervalul_de_afisare=1.33 )
dt: .3
Afisarea
rezultatelor la interval de (minute): 1.33
Intervalul de
afisare nu este un multiplu de dt !
Timp Temperatura
0 25.00
39.90 12.01
79.80 10.27
Ex. :
Sa se calculeze si sa se reprezinte grafic functiile :
a) 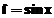 daca
daca 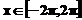 , cu pasul de indexare de 0,1;
, cu pasul de indexare de 0,1;
b)  cu pasul de indexare de -0,3.
cu pasul de indexare de -0,3.
a) Cu sintaxa Matlab :
» x=-2*pi:0.1:2*pi;
» f=sin(x);
» plot(x,f)
se obtin valorile functiei f, care vor fi afisate daca se tasteaza, in linia de
comanda, numele acesteia, si, intr-o fereastra grafica Figure 1 reprezentarea functiei f :
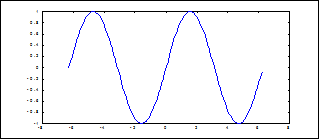
b) Pentru functia g se foloseste secventa de program:
» m=25:-0.3:-10;
» for k=1:length(m)
if
(m(k)>=-10)&(m(k)<=2)
g(k)=exp(m(k))+2
elseif
(m(k)>2)&(m(k)<=8)
g(k)=-2
elseif
(m(k)>8)&(m(k)<=25)
g(k)=(log(m(k)^2-5^(1/7))+19)/log(3)
end
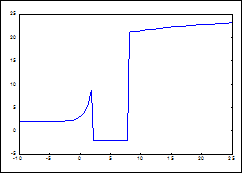 end
end
» plot(m,g)
Se obtin valorile indexate ale functiei g si
graficul din figura alaturata :
Ex. : Un
fisier script care genereaza « petale » :
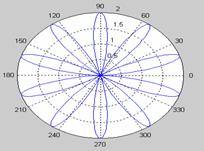 theta = -pi:0.01:pi;
theta = -pi:0.01:pi;
rho(1,:) =
2*sin(5*theta).^2;
rho(2,:) =
cos(10*theta).^3;
rho(3,:) =
sin(theta).^2;
rho(4,:) =
5*cos(3.5*theta).^3;
for i = 1:4
polar(theta,rho(i,:))
pause
end
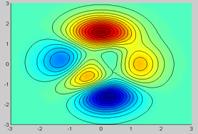 Ex.: O secventa de instructiuni care
genereaza zone de culoare cu intensitati diferite :
Ex.: O secventa de instructiuni care
genereaza zone de culoare cu intensitati diferite :
[x,y,z] = peaks;
contour(x,y,z,20,'k')
hold on
pcolor(x,y,z)
shading interp
hold off
Ex. : O secventa de instructiuni care imparte
o figura in mai multe parti:
 t = 0:pi/10:2*pi;
t = 0:pi/10:2*pi;
[X,Y,Z] =
cylinder(4*cos(t));
subplot(2,2,1);
mesh(X)
subplot(2,2,2);
mesh(Y)
subplot(2,2,3);
mesh(Z)
subplot(2,2,4);
mesh(X,Y,Z)
Ex. : O
secventa de instructiuni care genereaza o matrice:
m=4;n=3;
for i = 1:m
for j = 1:n
A(i,j) = 1/(i + j -
1);
end
end
A =
Columns 1 through 8
1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250
0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111
0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000
0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909
0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.0833
Ex.: Un fisier care genereaza o matrice:
for i = 1:10
A(i,i) = 1; % se introduce cifra " ", pe diagonala principala
if (i > 1)
A(i,i-1) = 2; % se introduce
cifra " 2", in fata diagonalei
principale, dar numai pe ultimele 9 linii,
end
if (i < 10)
A(i,i+1) = 5; % se
introduce cifra " 5", in dreapta
diagonalei principale, dar numai pe primele 9 linii,
end
end
Daca
se tasteaza numele matricei ("A"),
se afiseaza urmatorul rezultat:
A =
1 5 0 0 0 0 0 0 0 0
2 1 5 0 0 0 0 0 0 0
0 2 1 5 0 0 0 0 0 0
0 0 2 1 5 0 0 0 0 0
0 0 0 2 1 5 0 0 0 0
0 0 0 0 2 1 5 0 0 0
0 0 0 0 0 2 1 5 0 0
0 0 0 0 0 0 2 1 5 0
0 0 0 0 0 0 0 2 1 5
0 0 0 0 0 0 0 0 2 1
Ex.: Un fisier script de operare cu matrici:
m1=[-4 1 0; 1 -4 1;
0 1 -4]
m2=eye(3)
m3=zeros(3,3)
a=[m1 m2 m3; m2 m1
m2; m3 m2 m1]
b=[-100; -100;
-100; 0; 0; 0; 0; 0; 0]
ab
b = ans =
-100 42.8571
-100 52.6786
-100 42.8571
0 18.7500
0 25.0000
0 18.7500
0 7.1429
0 9.8214
0 7.1429
|
|
a =
-4 1 0 1 0 0 0 0 0
1 -4 1 0 1 0 0 0 0
0 1 -4 0 0 1 0 0 0
1 0 0 -4 1 0 1 0 0
0 1 0 1 -4 1 0 1 0
0 0 1 0 1 -4 0 0 1
0 0 0 1 0 0 -4 1 0
0 0 0 0 1 0 1 -4 1
0 0 0 0 0 1 0 1 -4
Ex. : Un fisier script de operare cu matrici:
k(1)=1.5;
k(2)=1;
k(3)=1.5;
k(4)=2;
l(1)=0.3;
l(2)=0.1;
l(3)=0.2;
l(4)=0.2;
b=zeros(4,1);
for i=1:3
b(i)=k(i)*l(i)-k(i+1)*l(i+1);
end
b(4)=1;
m=zeros(4,4);
for i=1:3
m(i,i)=k(i)+k(i+1);
m(i+1,i)=-k(i+1);
m(i,i+1)=-k(i+1);
end
m(4,4)=1;
m(4,3)=0;
b
m
x=mb
Rezultatele sunt :
| | | |
| |
m =
2.5000 -1.0000
0 0
-1.0000 2.5000
-1.5000 0
0 -1.5000 3.5000 -2.0000
0
0 0 1.0000
|
|
|
b =
0.3500
-0.2000
-0.1000
1.0000
|
|
|
x =
0.3471
0.5176
0.7647
1.0000
|
|
Ex. : Un fisier script de operare cu matrici:
coord(1,1)=-0.6;
coord(1,2)=0;
coord(2,1)=-0.9;
coord(2,2)=1.5;
coord(3,1)=-1.6;
coord(3,2)=1.8;
coord(4,1)=0;
coord(4,2)=2.7;
coord(5,1)=1.6;
coord(5,2)=1.8;
coord(6,1)=0.9;
coord(6,2)=1.5;
coord(7,1)=0.6;
coord(7,2)=0;
c(1,1)=1;
c(1,2)=2;
c(2,1)=2;
c(2,2)=3;
c(3,1)=3;
c(3,2)=4;
c(4,1)=4;
c(4,2)=5;
c(5,1)=5;
c(5,2)=6;
c(6,1)=6;
c(6,2)=7;
c(7,1)=7;
c(7,2)=8;
m=zeros(7,7);
for i=1:7
if
c(i,1)~=1
if c(i,1)==8
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
elseif
c(i,1)==7
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
m(11,i)=(coord(c(i,1),1)-coord(c(i,2),1))/dist;
else
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
m(2*c(i,1)-3,i)=(coord(c(i,1),1)-coord(c(i,2),1))/dist;
m(2*c(i,1)-2,i)=(coord(c(i,1),2)-coord(c(i,2),2))/dist;
end
end
if
c(i,2)~=1
if c(i,2)==8
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
elseif
c(i,2)==7
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
m(11,i)=(coord(c(i,2),1)-coord(c(i,1),1))/dist;
else
dist=((coord(c(i,1),1)-coord(c(i,2),1))^2+(coord(c(i,1),2)- coord(c(i,2),2))^2)^0.5;
m(2*c(i,2)-3,i)=(coord(c(i,2),1)-coord(c(i,1),1))/dist;
m(2*c(i,2)-2,i)=(coord(c(i,2),2)-coord(c(i,1),2))/dist;
end
end
end
m
b=zeros(11,1);
b(4,1)=-10;
b
d=mb
% FINAL PROGRAM
Acest fisier script, introdus
in linia de comanda a MATLAB, la apasarea tastei ENTER, va avea ca
efect afisarea urmatoarelor rezultate:
m =
-0.1961 0.9191 0 0 0 0 0
0.9806 -0.3939 0 0 0 0 0
0 -0.9191 -0.8716 0 0 0 0
0 0.3939 -0.4903 0 0 0 0
0 0 0.8716 -0.8716 0 0 0
0 0 0.4903 0.4903 0 0 0
0 0 0 0.8716 0.9191 0 0
0 0 0 -0.4903 0.3939 0 0
0 0 0 0 -0.9191 0.1961 0
0 0 0 0 -0.3939 0.9806 0
0 0 0 0 0 -0.1961 0.3714
b =
0
0
0
-10
0
0
0
0
0
0
0
d =
-2.1265
-3.7535
3.8868
1.1340
-0.4106
-0.2326
-0.1228
Ex. :
Un fisier pentru calculul elementelor
traiectoriei unui proiectil (viteza, inaltime,
distanta) lansat sub un anumit unghi fata de orizontala,
sub actiunea gravitatiei:
dt = 0.1;
g = 9.8;
u = 60;
Alfa = input( 'Introduceti unghiul de lansare al proiectilului: '
);
Radian = Alfa * pi / 180; % conversia in radiani
x_initial = zeros(1); y_initial = zeros(1); % initializare
y = 0; t = 0;
i = 1; % initial vector subscript
while y >= 0
t = t + dt;
i = i + 1;
y = u * sin(Radian) * t - g * t^2 / 2;
if y >= 0
Distanta_pe_x(i) = u * cos(Radian) * t;
Inaltimea_pe_y(i) = y;
end
end
plot(Distanta_pe_x, Inaltimea_pe_y,'k'), grid on
Introduceti unghiul de lansare al
proiectilului: 50

APLICATII
Ex.1:
Sa se compare elementele
matricei  cu
scalarul B=
cu
scalarul B=  ;
;
Ex.2:
Sa se compare elementele
matricei  cu elementele
matricei
cu elementele
matricei 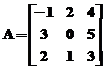 ;
;
Ex.3:
Sa se compare elementele
matricelor 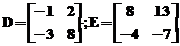 ;
;
Ex.4:
Sa se compare elementele
matricelor 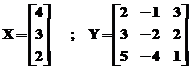 cu scalarul
cu scalarul  ;
;
Ex.5:
Sa se realizeze un
fisier script pentru afisarea unei matrici cu dimensiunea 3x4 in care
elementele primei linii sa difere printr-o constanta, numar
natural, elementele celei de-a doua linii sa difere prin constanta e2,
iar elementele ultimei linii sa difere prin ln8.
Ex.6:
Sa se actualizeze
fisierul de mai jos astfel incat sa se afiseze inca
doua butoane la alegere :
k=0;
while k~=3
k=menu('Faceti clic pe una dintre
optiuni','Fa asta','Fa alta', 'Iesire');
if k==1
disp('Fa astaApasa orice cheie pentru a
continua')
pause
elseif k==2
disp('Fa altaApasa orice cheie pentru a
continua')
pause
end
end
Ex.7:
Sa se actualizeze fisierul
de mai jos astfel incat sa se afiseze inca doua subgrafice,
cu titlurile (c) si (d):
subplot(2,2,1)
plot(rand(1, 20)),title('(a)')
subplot(2,2,2)
axis([0 4 0 4])
plot([0 4], [0 0], [1 1 2 3 3], [0 2 3 2 0]),title('(b)')

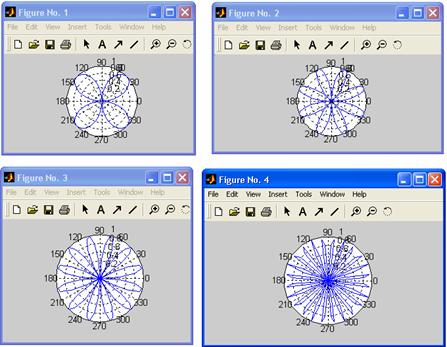
Ex.8:
Sa se actualizeze fisierul
de mai jos astfel incat sa se afiseze 8, 12, 24 de "petale":
x = 0:pi/40:2*pi;
polar(x, sin(2*x)),grid
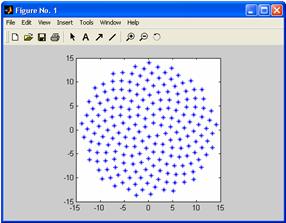
Ex.9:
Sa se actualizeze
fisierul de mai jos astfel incat sa se solicite utilizatorului
sa introduca diametrul "desenului":
n=1:200;
d = 137.51;
th = pi*d*n/180;
r = sqrt(n);
plot(r.*cos(th), r.*sin(th),
'*')
axis square
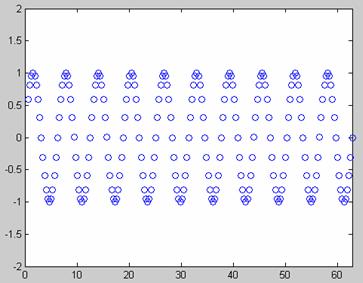
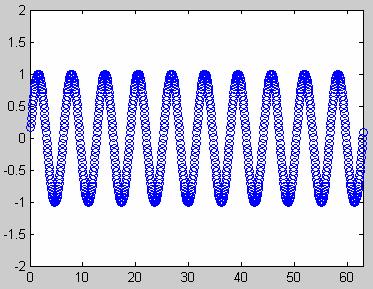
Ex.9:
Sa se actualizeze fisierul
de mai jos astfel incat "pasul de desenare" sa fie mai mic, respectiv, in
alta varianta, sa fie mai mare:
x = 0;
y = 0;
dx = pi/100;
p = plot(x, y, 'o',
'EraseMode', 'none'); % 'xor' afiseaza numai punctele curente
% ' none' afiseaza
toate punctele
axis([0 20*pi -2 2])
for x = dx:dx:20*pi;
x = x + dx;
y = sin(x);
set(p, 'XData', x, 'YData', y)
pause(0.05)
end
Ex.9:
Sa se actualizeze fisierul
de mai jos astfel incat "sombrero-ul" sa fie inclinat spre stanga sau spre
dreapta, si "lumina" sa "cada" din dreapta :
[x y ] = meshgrid(-8 : 0.5 :
8);
r = sqrt(x.^2 + y.^2) + eps;
z = sin(r) ./ r;
surf(x,y,z,'facecolor','interp','edgecolor','none',
'facelighting','phong')
colormap jet
daspect([10 5 1])
axis tight
view(-50, 30)
camlight right
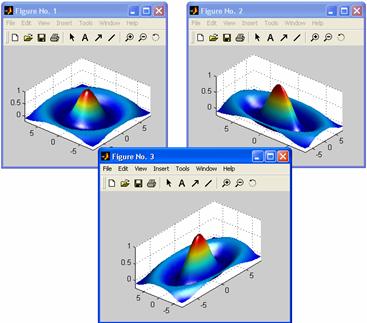
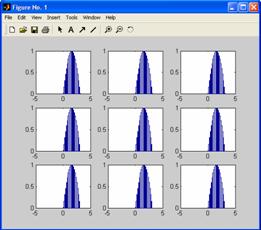
Ex.10:
Sa se actualizeze fisierul
de mai jos astfel incat imaginea reprezentarii grafice sa fie
amplasata pe o "matrice" grafica de 3 linii si 3 coloane (ca in
figura):
subplot(3,3,1)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted,
subplot(3,3,2)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted,
subplot(3,3,3)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,4)
 x =
0:pi/20:pi;
x =
0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,5)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,6)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,7)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,8)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
subplot(3,3,9)
x = 0:pi/20:pi;
bar(x,sin(x),'w'), shading faceted
Ex.11:
Sa se actualizeze fisierul
de mai jos astfel incat utilizatorul sa fie solicitat sa
introduca viteza initiala si timpul total al
miscarii
g = 9.8;
 v0
= 60;
v0
= 60;
t = 0 : 0.1 : 12.3;
s = v0 * t - g / 2 * t .^ 2;
plot(t, s), title( 'Miscarea pe verticala sub
actiunea gravitatiei' )
xlabel( 'Timpul' ), ylabel( 'Inaltimea' ),
grid
disp( [t' s'] )
capitolul v
CALCULE NUMERICE CU POLINOAME
Pentru
operarea cu polinoame, MATLAB utilizeaza functiile standard din
tabelul urmator:
|
Functia
|
Descriere
|
|
conv(p,q)
|
-produsul polinoamelor p si q
|
|
[C,R]=deconv(p,q)
|
-Catul, C,
si restul R al impartirii polinoamelor p si q
|
- poly(r)
- poly(A)
|
- -determina polinoamele cu radacini date in
vectorul coloana r
-determina coeficientii polinomului caracteristic ai
matricei patratice A
|
- polyder(p)
- polyder(p,q)
- [A,B]=polyder(p,q)
|
- -derivata polinomului p
- -derivata produsului polinoamelor p si q
- -derivata fractiei rationale p/q
|
- polyfit(x,y,n)
- [p,S]=polyfit(x,y,n)
- [p,S,miu]=polyfit(x,y,n)
|
- aproximeaza un set de date x si y cu un
polinom de gradul n
- aproximeaza un set de date x si y cu un
polinom de gradul n
- aproximeaza un set de date x si y cu un
polinom de gradul n
|
|
polyval(p,x)
polyval(p,q)
|
- evaluarea polinomului p in
punctul x, sau pe intervalul x
- evaluarea polinomului p in
punctele vectorului q
|
|
polyvalm(A)
|
-evaluarea polinomului in elementele matricei
patratice A
|
|
[r,p,k]=residue(a,b)
|
-descompunerea raportului a doua polinoame a si b in fractii simple, avand ca rezultat vectorul
coloana al reziduurilor, r,
vectorul coloana al polilor, p,
si k - vectorul linie al
polinomului cat (A/B)
|
|
roots(p)
|
-calculeaza radacinile unui polinom p
|
Reprezentarea polinoamelor
Polinoamele
sunt reprezentate, in MATLAB, ca vectori linie, continand
coeficientii ordonati dupa puterile descrescatoare ale
variabilei. Forma generala
a polinoamelor, in scrierea algebrica:
f(x) = anxn+an-1xn-1+..+a2x2+a1x+a0
iar reprezentarea acestuia, in
MATLAB, este data prin vectorul linie f=[a_n,a_n_1,,a2,a1,a0],
in care elementele sunt reprezentate de coeficientii polinomului de grad n. De exemplu, polinomul p(x)=x4 +7x3+x-8
se introduce astfel:
»p=[1,7,0,1,-8]
Ex. : Fie
polinoamele: f(x) = x3+2x2+0,5x-6,5
; h(x)=x5+2x2-6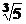
Aceste polinoame se scriu, in MATLAB:
»f = [1,2, 0.5, -6.5];
»h=[1,0,0,2,0,-6*(5^(1/3))];
Obs.: In polinomul h(x) coeficientii lui x4, x3 respectiv x,
care lipsesc, sunt inlocuiti cu
valoarea 0 (zero). Altfel, MATLAB
va introduce un polinom de grad inferior celui
real (de exemplu, daca h(x) ar fi introdus de la tastatura numai cu
coeficientii h=[1,2,-6*(5^(1/3))]
acesta reprezinta polinomul h(x)=x2+2x--6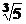 )
)
Produsul polinoamelor
Produsul
a doua polinoame se realizeaza, in MATLAB,
folosind functia conv() :
»c = conv(a, b)
unde :
a, b - vectorii coeficientilor
polinoamelor care se inmultesc
Ex. :
Sa se calculeze produsul
: g(x)
= (x2+x-2)(x+1)
-in MATLAB:
»g1
= [1 1 -2];
»g2
= [1 1];
»g
= conv(g1, g2)
g
= [1 2 -1 -2]
care in
forma algebrica uzuala se scrie : g(x) = x3+2x2-x-2
Impartirea polinoamelor
Pentru
realizarea impartirii a doua polinoame se foloseste
functia MATLAB deconv() :
» [c, r] = deconv(a, b)
in care :
c - vectorul coeficientilor
polinomului cat
r - vectorul coeficientilor
polinomului rest
Polinoamele c(x) si r(x) respecta teorema impartirii cu rest ( p(x)=d(x)*c(x)+r(x), in care p(x)
este polinomul- "deimpartit", d(x)
reprezinta polinomul- "impartitor" :
p(x)=d(x)*c(x)+r(x), in care p(x)
este polinomul- "deimpartit", d(x)
reprezinta polinomul- "impartitor" : 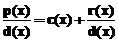 )
)
Ex. : Sa se
calculeze catul si restul impartirii polinoamelor h1(x)= x3+2x2-2
si h2(x)= x2+x,
folosind o functie MATLAB.
-in
MATLAB:
»h1 = [1 2 0 -2];
»h2 = [1 1 0];
»[c, r] = deconv(h1, h2)
c =
1 1
r =
0 0 -1 -2
In format algebric uzual catul
impartirii este: c(x)=x+1,
iar restul r(x)= -x-2 .
Determinarea radacinilor unui polinom
Determinarea
radacinilor unui polinom, se realizeaza folosind functia
MATLAB roots() :
»r = roots(a)
in care:
a - vector linie al coeficientilor
polinomului
Ex. : Fie polinomul f(x) = x3-2x2-3x+10.
Sa se determine radacinile ecuatiei f(x)=0.
in
MATLAB
»f = [1 -2 -3 10]
»r=roots(f)
T se obtine vectorul
coloana al radacinilor
r =
2+i
2-i
-2
Determinarea coeficientilor polinoamelor
daca se cunosc radacinile
Determinarea
unui polinom, daca se cunosc radacinile acestuia, se
utilizeaza functia MATLAB poly():
» p = poly(z)
in care:
z - vectorul- coloana al
radacinilor
Ex. :
Fie
radacinile unui polinom : x1=2;
x2=3; x3=4. Sa se determine polinomul cu
radacinile x1; x2;
x3.
Problema se va
rezolva prin doua metode:
a)-algebric-clasic:folosind sumele
Viète
b)-in MATLAB: folosind functia poly()
a) Solutia
algebrica:
Folosind
relatiile Viète, se obtin sumele:
S1 = x1+x2+x3
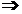 S1= 9
S1= 9
S2 = x1x2+x1x3+x2x3
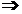 S2=26
S2=26
S3 = x1x2x3 
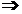 S3= 24
S3= 24
Polinomul cu
radacinile x1; x2; x3 se scrie, folosind forma generala a unui
polinom (pentru care se cunosc sumele Viète p(x)=xn-S1xn-1+S2xn-2--Sn
) p(x)
= x3-9x2+26x-24.
b)
Rezolvare cu functia poly():
Folosind
functia MATLAB poly(), rezolvarea este imediata:
» b=[2;3;4];
» p=poly(b)
p =
1 -9 26 -24
Polinomul p(x), in format
algebric, uzual, se scrie p(x) = x3-9x2+26x-24 .
Cu
functia poly(), se
determina si coeficientii polinomului caracteristic al unei
matrici patratice. De exemplu, cu secventa urmatoare, se determina
polinomul ale carui radacini (se mai numesc si radacini
caracteristice) sunt valorile proprii ale matricei (valorile proprii
ale matricei se determina cu functia MATLAB eig()):
» A = [1.2 3 -0.9; 5 1.75 6; 9 0 1];
» p=poly(A)
p =
1.0000 -3.9500 -1.8500 -163.2750
»radacini=roots(p)
radacini =
7.2826
-1.6663 + 4.4321i
-1.6663 - 4.4321i
» valorile_proprii=eig(A)
valorile_proprii =
7.2826
-1.6663 + 4.4321i
-1.6663 - 4.4321i
Evaluarea numerica a unui polinom
1) Evaluarea simpla:
Se
foloseste in cazul in care polinomul are o expresie simpla si
valoarea atribuita variabilei este un scalar.
Ex. 6: Sa se calculeze valoarea polinomului f(x) = 3x4-5x3+3x-1 in punctul x = 2.
In
MATLAB, se declara, mai intai, valoarea variabilei, apoi se introduce
polinomul de evaluat, folosind regulile standard:
» x = 2;
» f =
3*(x^4)-5*(x^3)+3*x-1
f =
13
2) Evaluarea numerica element cu element
Cand variabila
in care se evalueaza polinomul este un vector sau o matrice problema se
rezolva respectand regulile de calcul cu matrici si tablouri de
valori:
a)- daca
variabila este un vector (linie sau coloana), calculul valorii polinomului
se poate realiza numai daca expresia polinomului este introdusa de la
tastatura utilizand regulile pentru calculul cu tablouri de valori
(variabila este considerata de MATLAB un tablou de valori, deci se va
folosi caracterul " . " -punct, pentru operatiile in care
este implicata variabila) altfel, MATLAB afiseaza un mesaj de
eroare:
???
Error using ==> ^
Matrix must be square.
???
Eroare la utilizarea ^
Matricile
trebuie sa fie patratice
Ex. :
1)-variabila este
un vector linie:
» x= [1 2 0];
» f =
3*x.^4-5*x.^3+3*x-1
f =
0 13 -1
Obs.:Daca
polinomul este introdus fara caracterul punct " .
" in fata operatorului pentru ridicare la putere:
» f = 3*x^4-5*x^3+3*x-1
MATLAB afiseaza mesajul:
??? Error using ==> ^
Matrix must be square.
Ex. :
2)-variabila este
un vector coloana:
»
x=[1;2;0];
» f = 3*x.^4-5*x.^3+3*x-1
f =
0
13
-1
b)- daca
variabila este o matrice patrata, iar expresia ce urmeaza a fi
evaluata este introdusa de la tastatura netinand cont de
modul de lucru cu tablouri de valori, expresia este calculata astfel: se
determina "puterile" matricei dupa
care sunt inmultite cu coeficientii, rezultatele acestor
inmultiri fiind, apoi, insumate algebric, solutia fiind, evident, o
matrice de aceeasi dimensiune ca si variabila. In acest caz,
polinomul f(x) devine f(x),
iar termenul liber a0 devine a0*I (unde I este matricea unitate de ordin egal
cu ordinul matricei X):
Ex. :
» x=[1,2;3,4];
» f = 3*x^4-5*x^3+3*x-1
f =
414 605
908 1323
c)- daca
variabila este un tablou de valori (numarul de linii diferit de
numarul de coloane), expresia de evaluat trebuie introdusa de la
tastatura folosind regulile de calcul specifice tablourilor de valori
(operatorii: " .^ " sau " .* ") altfel MATLAB afiseaza
un mesaj de eroare:
Ex. 10 :
» x=[1,2,3;4,5,6];
» f = 3*x.^4-5*x.^3+3*x-1
f =
0 13 116
459 1264 2825
Obs.: Daca
expresia f(x) se introduce:
» f = 3*x^4-5*x^3+3*x-1
MATLAB afiseaza mesajul :
???
Error using ==> ^
Matrix
must be square.
Evaluarea polinoamelor cu
functia MATLAB polyval(p,
q)
Evaluarea
expresiilor polinomiale, in MATLAB, se poate realiza folosind functia polyval():
» f = polyval(p, q)
sau
»f=polyvalm(p,q)
in care:
p - vectorul linie al
coeficientilor polinomului;
q - vectorul , respectiv, matricea in care
se evalueaza polinomul p.
Ex. :
Sa se
determine valoarea polinomului p(x)=3x4+x3+2x2-1
in punctele vectorului q=[1,2,3,4,0],
respectiv ale matricelor Q = [1 2 ; 3 4] si R =
[1 2 3 ; 3 4 5].
In MATLAB:
» p = [3 1 2 0 -1];
» q = [1 2 3 4 0]; Q = [1 2 ; 3 4]; R = [1 2 3 ; 3 4 5];
» f1=polyval(p,q)
f 1=
5 63 287 863 -1
» f2=polyval(p,Q)
f2 =
5 63
287 863
» f3=polyvalm(p,Q)
f3 =
647 944
1416 2063
» f4=polyval(p,R)
f4 =
5 63 287
287 863 2049
» f5=polyvalm(p,R)
??? Error using ==> polyvalm
Matrix must be square.
Evaluarea pe intervale
Daca se cere evaluarea unui
polinom pe un interval in n puncte:
-
se imparte intervalul in n puncte,
dupa o regula prestabilita;
-
se evalueaza polinomul folosind functia MATLAB polyval().
Ex. :
Sa se
determine valoarea polinomului p(x)=3x4+x3+2x2-1,
pentru valorile x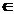 [0,5] in punctele fixe distantate la 0,2 unitati.
[0,5] in punctele fixe distantate la 0,2 unitati.
In MATLAB:
» x = 0:0.2:5; p = [3 1 2 0 -1];
» f = polyval(p, x)
f =
1.0e+003 *
Columns 1 through 10
-0.0010 -0.0009 -0.0005 0.0003 0.0020 0.0050 0.0098 0.0172 0.0279 0.0428
Columns 11 through 20
0.0630 0.0896 0.1239 0.1672 0.2210 0.2870 0.3668 0.4623 0.5755 0.7083
Columns 21 through 26
0.8630 1.0419 1.2473 1.4819 1.7482 2.0490
Calculul derivatei
Derivata polinomului
Derivata
polinomului se calculeaza folosind functia MATLAB polyder():
» D = polyder(c)
in care:
c - vectorul linie al
coeficientilor
Ex. :
Sa se
calculeze derivata polinomului A(x) = x3+2x2-x+2
» A = [1 2 -1 2]
» D = polyder(A)
D =
3 4 -1
Derivata produsului a doua
polinoame
Prin
definitie, derivata produsului a doua polinoame este tot un polinom,
obtinut prin relatia:
( A(x) · B(x) )' = A'(x) · B(x) + A(x) · B'(x).
Asadar, calculul acestei derivate implica folosirea
aceleiasi functii MATLAB polyder(),
in care, argumentul de intrare (inscris, intotdeauna, intre paranteze
rotunde), este format din vectorii linie ai coeficientilor celor doua
polinoame:
» D = polyder(A, B)
Ex. Sa se determine
derivata produsului (x3+2x2-x+2) · (x-1).
In MATLAB:
» A = [1 2 -1 2]; B = [1 -1];
» D_prod = polyder(A, B)
D_prod =
4 3 -6 3
Derivata catului a doua
polinoame
Se
cunoaste faptul ca derivata catului a doua polinoame este o
expresie rationala. In consecinta, functia MATLAB,
pentru calculul derivatei catului a doua polinoame se introduce cu
parametri de iesire (parametrii de iesire, in acest caz numaratorul respectiv numitorul expresiei rationale
rezultati ca urmare a calculului derivatei, se introduc in linia de
comanda intre paranteze drepte, in partea stanga a semnului de
atribuire, " = " ). Pentru calculul derivatei catului a doua polinoame se
foloseste functia MATLAB polyder():
» [M, N] = polyder(A, B)
in care:
-M si N sunt polinoamele de la numaratorul respectiv numitorul
expresiei derivate;
-A si B sunt polinoamele de la numaratorul respectiv numitorul
expresiei ce urmeaza a fi
derivata.
Ex. :
Sa se
determine derivata expresiei rationale: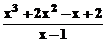 .
.
In MATLAB:
» A = [1 2 -1 2]; B = [1 -1];
» [M, N] = polyder(A, B)
M =
2 -1 -4 -1
N =
1 -2 1
In format algebric uzual,
rezultatul se scrie: 
Adunarea si scaderea polinoamelor
Aceste
operatii se pot executa numai daca polinoamele au acelasi grad,
prin urmare polinoamele trebuie transformate, prin extindere spre stanga,
astfel incat acestea sa fie de acelasi grad. Dupa uniformizarea
gradului, adunarea algebrica a polinoamelor se realizeaza, in MATLAB,
ca o insumare a doi vectori de aceeasi dimensiune.
Ex. :
Sa
se calculeze suma si diferenta polinoamelor: g(x) = x4-5x2+6x-1 si h(x) = x3+3x-2.
In
MATLAB, intrucat polinomul h(x) are
gradul III, acesta va fi "adus" la gradul IV corespunzator polinomului g(x) prin impunerea unui coeficient
"fals" (zero):
Astfel:
» g = [1 0 -5 6 -1];
h = [0 1 0 3 -2];
» sum = g+h
sum =
1 1 -5 9 -3
» dif = g-h
1 -1 -5 3 1
Descompunerea in fractii simple
Orice expresie
rationala, 
 se poate descompune in
fractii simple, dupa radacinile polinomului de la numitor (solutiile numitorului se numesc poli):
se poate descompune in
fractii simple, dupa radacinile polinomului de la numitor (solutiile numitorului se numesc poli):

Obs.: Daca polul pj are ordinul m
de multiplicitate expresia se scrie:
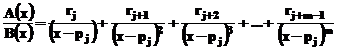
Intrucat
descompunerea in fractii simple are ca rezultat trei vectori, functia
MATLAB residue, se introduce cu parametri de iesire. Functia MATLAB pentru
descompunerea in fractii simple este:
» [r, p, k] = residue(A, B)
in care:
r - vectorul coloana al
reziduurilor;
p - vectorul coloana al polilor;
k - vectorul linie al polinomului cat (A/B)
Ex. :
Sa se descompuna in
fractii simple urmatoarea expresie: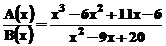 .
.
In MATLAB (se vor calcula, pentru
comparatie, catul polinoamelor A(x), B(x); catul si restul
impartirii polinoamelor A(x), B(x) si apoi, se va descompune in
fractii simple expresia A(x)/ B(x)) :
» A = [1 -6 11 -6];
» B = [1 -9 20];
» [Catul,Restul]=deconv(A,B)
Catul =
1 3
Restul =
0 0 18 -66
» [reziduuri_partiale, polii_fractiei,
coeficientii_catului] = residue(A,B)
reziduuri_partiale =
24
-6
polii_fractiei =
5
4
coeficientii_catului =
1 3
Acest rezultat poate fi
transcris, in format algebric, astfel:
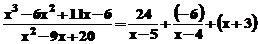


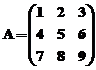 cu scalarul
cu scalarul 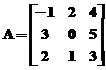 si
si 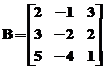 .
. , pentru valorile intregi ale variabilei x.
, pentru valorile intregi ale variabilei x.
 cu pasul de indexare de -0,3.
cu pasul de indexare de -0,3.
 end
end theta = -pi:0.01:pi;
theta = -pi:0.01:pi;  Ex.: O secventa de instructiuni care
genereaza zone de culoare cu intensitati diferite :
Ex.: O secventa de instructiuni care
genereaza zone de culoare cu intensitati diferite : t = 0:pi/10:2*pi;
t = 0:pi/10:2*pi;
 cu
scalarul B=
cu
scalarul B=  cu elementele
matricei
cu elementele
matricei 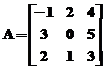 ;
; 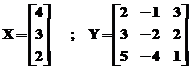 cu scalarul
cu scalarul