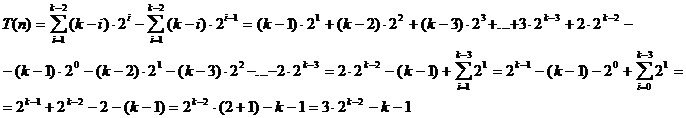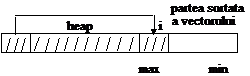Problema Sortarii

Sortarea ese o operatie foarte des intalnita in rezolvarea unei probleme prin metode algoritmice. Din acest motiv algoritmii de sortare constituie o clasa extrem de importanta care merita o atentie speciala iar o analiza a celor mai cunoscuti algoritmi de sortare este utila si necesara.

Bubble Sort sortare prin interschimbare

Bubble_sort (A,n)

// A[1..n] - seceventa de sortat

}

Complexitatea: Evident O(n²)

Insertion Sort (sortare prin inserare)

Algoritmul Insertion Sort considera ca in pasul k, elementele A[1÷k‑1] sunt sortate, iar elementul de pe pozitia k va fi inserat, astfel incat, dupa aceasta inserare, primele elemente A[1÷k] sa fie sortate.

Pentru a realiza inserarea elementului k in secventa A[1÷k‑1], aceasta presupune:

memorarea elementului intr‑o variabila temporara;

deplasarea tuturor elementelor din vectorul A[1÷k‑1] care sunt mai mari decat A[k], cu o poziie la dreapta (aceasta presupune o parcurgere de la dreapta la stanga);

plasarea lui A[k] in locul ultimului element deplasat.

insertion_sort(A,n)

A[i+1] = temp;

}

Complexitatea:

Cazul cel mai dafavorabil: situatia in care deplasarea (la dreapta cu o pozitie in vederea inserarii) se face pana la inceputul vectorului, adica sirul este ordonat descrescator.

Exprimarea timpului de lucru:

T(n) = 3·(n - 1) + (1 + 2 + 3+ + n - 1) = 3(n-1) + 3n (n - 1)/2

Rezulta complexitatea: T(n) = O(n²) functie polinomiala de gradul II.

Observatie: Cand avem mai multe bucle imbricate, termenii buclei celei mai interioare dau gradul polinomului egal cu gradul algoritmului.

Bucla cea mai interioara ne da complexitatea algoritmului.

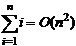
Shell Sort sortare prin metoda Shell

Sortarea se face asupra unor subsecvente care devin din ce in ce mai mari pina la dimensiunea n. Fiecare subsecventa i o este determinata de un h_i numit increment.

Incrementii satisfac conditia : h_t > h_t-1 > . > h₂ > h₁

Fie h_i = h. Avem urmatoarele subsecvente:

A[1], A[1+h], A[1+2h], . A[1+kh];

A[2], A[2+h], A[2+2h], .

_{. . . . . .}

A[h], A[h+h], A[1+2h], .

Exemplu :

h=4 1 5 7 8 3 12 9 4 12

|_____ _______ ______ _____________|_____ _______ ______ ______________|

|_____ _______ ______ _____________|

|_____ _______ ______ _____________|

|_____ _______ ______ _____________|

h=3 1 5 7 8 3 12 9 4 12

|_____ _______ ______ ______|_____ _______ ______ ______|

|_____ _______ ______ ______|_____ _______ ______ ______|

|_____ _______ ______ ______|_____ _______ ______ ______|

h=1 1 5 7 8 3 12 9 4 12

|_______|_______|_______|_______|_______|______|_______|_______|

Shell_sort (A,n,h,t);

// A[1..n] - seceventa de sortat

// H[1..t] - incrementii h_t > h_t-1 > . >h₁=1

A[i+h]=x;

}

}

Complexitatea:

Greu de esitimat. Se presupune (din analiza rezultatelor experimentale) ca ar fi n^1,2.

Radix Sort

Se presupune ca cheile de sortare sint numere intregi. Fiecare element din secventa de sortat are k cifre c₁c₂ . c_k

radix_sort (A,n,k)

// se presupune ca numerele intregi sint reprezentate in baza b<=10

// secventa se afla intr-o coada globala gq iar q[j], j=0, . ,b-1 sunt cozi;

for j=0, . ,b-1

while ( not isempty(q[j]) ) //adauga coada q[j] la cooda globala gq

add (gq,del(q[j])

}

for i=1, . ,n;

A[i]=del[gq];

Complexitatea:

O(nk)

Heap_Sort

Definitie:Se numeste arbore heap un arbore binar T = (V, E) cu urmatoarele proprietati:

functia key : V R care asociaza fiecarui nod o cheie.

un nod v V cu degree(v) > 0 (nu este nod terminal), atunci:

key(v) > key(left_child(v)), daca left_child(v)

key(v) > key(right_child(v)), daca right_child(v)

(Pentru fiecare nod din arbore, cheia nodului este mai mare decat cheile descendentilor).

Observatie: De obicei functia cheie reprezinta selectia unui subcamp din campul de date memorate in nod.

Generare Heap

Generare Heap prin inserari repetate

heap_gen_1 (A,V, n)

// A[1..n] - seceventa de sortat

// V vectorul ce contine reprezentarea heap-ului;

// N numarul de noduri din heap,

insert(V, N, a)

// V vectorul ce contine reprezentarea implicita a heap-ului;

// N numarul de noduri din heap,

// ambele sunt plasate prin referinta (functia insert le poate modifica);

// a atomul de inserat;

// 1) In reprezentarea implicita: V [N + 1] = a ; N = N + 1

// In continuare se reorganizeaza structura arborelui astfel incit sa-si pastreze structura de heap.

// 2) Se utilizeaza interschimbarile. Comparatii:

Se iau 2 indici: child = N si

parent = [N/2]

Se compara V[child] cu V[parent]

Interschimbare daca V[child] nu este mai mic decat V[parent]

// 3) Inaintare in sus:  child = parent

parent = [child/2]

// 4) Se reia pasul 2) pana cand nu se mai face interschimbarea.

else break; // se paraseste bucla parent = 0

}

Complexitatea:

Complexitatea operatiei insert:

In cazul cel mai defavorabil se parcurge o ramura care leaga un nod terminal de radacina. Rezulta, complexitatea este data de adancimea arborelui. Daca N este numarul de noduri din arbore, 2^k N < 2^k+1 , si adancimea arborelui este k+1.

2^k - 1 N < 2^k+1 - 1 k = log₂N

| |

| |

| |

nr. de noduri nr. de noduri

ale arborelui ale arborelui

complet de complet de

adancime k adancime k+1

k log₂N < k + 1 adancimea arborelui este k+1 = log₂N

Deci complexitatea este O(log N).

Complexitatatea algoritmului heap_gen_1

Se fac n-1 operatii insert in heap-uri cu dimensiunea N n

Rezulta complexitatea acestor operatii nu depaseste O(nlog n). Facem un studiu pentru a vedea daca nu cumva ea este mai mica decit O(nlog n)

Cazul cel mai defavorabil este situatia in care la fiecare inserare se parcurge o ramura completa. De fiecare data inserarea unui element se face adaugand un nod la ultimul nivel. Pentru nivelul 2 sunt doua noduri. La inserarea lor se va face cel mult o retrogradare (comparatie).

nivelul 2 : 2 noduri 1 comparatie

nivelul 3 : 4 noduri 2 comparatii

nivelul 4 : 8 noduri 3 comparatii

nivelul i  : 2^i-1 noduri i-1 comparatii

Considerand un arbore complet (nivel complet) n = 2^k - 1 numarul total de comparatii pentru toate nodurile este T(n) de la nivelul 2 la nivelul k. Vom calcula:

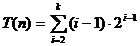
Sa aratam: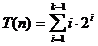  

cu tehnica 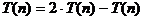  . Asadar:

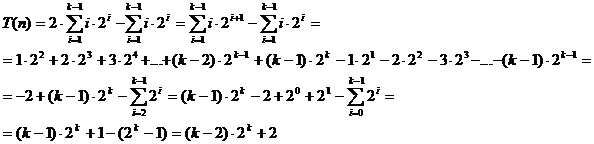
Rezulta: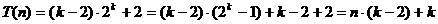 

iar:  ,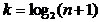

din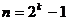

Rezulta: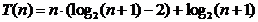 

----- ----- --------------

termen dominant

Facandu-se majorari, rezulta complexitatea O(nlog n) pentru Heap_Gen_1.

Generare Heap prin retrogradari repetate

Construim heap-ul de jos in sus (de la dreapta spre stanga). Cele mai multe noduri sunt la baza, doar nodurile din varf parcurg drumul cel mai lung.

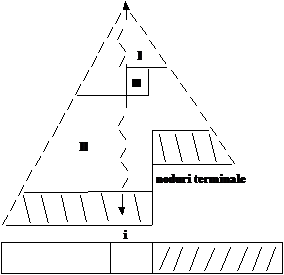
Presupunem ca elementele V[i+1,n] indeplinesc conditia de structura a heap-ului:

j >i avem:   V[j] > V[2*j] , daca 2*j n

V[j] > V[2*j +1] , daca 2*j + 1 n

Algoritmul consta in adaugarea elementului V[i] la structura heap-ului. El va fi retrogradat la baza heap-ului (prelucrare prin retrogradare):

heap_gen_2 (A,V, n)

// A[1..n] - secventa de sortat

// V vectorul ce contine reprezentarea heap-ului;

retrogradare(V, n, i)

else break;

}

Complexitatea

Fie un arbore complet cu n = 2^k - 1. Cazul cel mai defavorabil este situatia in care la fiecare retrogradare se parcurg toate nivelele:

nivel k : nu se fac operatii

nivel k-1 : 2^k-2 noduri o operatie de comparatie

nivel k-2 : 2^k-3 noduri 2 operatii

nivel i  : 2^i-1 noduri k-i operatii

nivel 2 : 2¹ noduri k-2 operatii

nivel 1 : 2⁰ noduri k-1 operatii

Se aduna, si rezulta: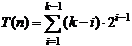  

Tehnica de calcul este aceeasi: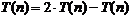

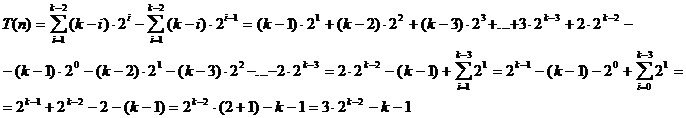
Rezulta: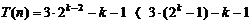   

-------

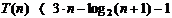
termen dominant

Rezulta complexitatea O(n) pentru heap_gen._2

Algoritmul Heap Sort

heap_sort (A,n)

// A[1..n] - secventa de sortat

Aceasta procedura sorteaza un vector A cu N elemente: transforma vectorul A intr-un heap si sorteaza prin extrageri succesive din acel heap.

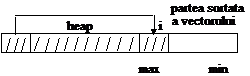
Procedura remove

remove(V, N)

// V vectorul ce contine reprezentarea implicita a heapu-lui;

// N numarul de noduri din heap

// ambele sunt plasate prin referinta (functia remove le poate modifica);

// se scoate elementul cel mai mare care este radacina heap-ului; se initializeaza cei 2 indici;

// se reorganizeaza structura arborilor: se ia ultimul nod de pe nivelul incomplet si-l aduc in nodul

// radacina, si aceasta valoare va fi retrogradata pina cand structura heap-ului este realizata.

// parent = max(parent, lchild, rchild).

Exista trei cazuri:

conditia este indeplinita deodata;

max este in stanga retrogradarea se face in stanga;

max este in dreapta retrogradarea se face in dreapta.

else break;

}

return(a);

Complexitatatea algoritmului heap_sort

Complexitatea algoritmului Heap_Sort este determinata de functiile remove ce nu pot fi aduse la complexitate < O(log n). Astfel: Heap_Sort = O(n) + O(n·log n)

----- ----- -----

termen ce determina complexitatea

Rezulta complexitatea alg. Heap_Sort = O(n·log n)

Merge_Sort si Quick_Sort

Merge_Sort si Quick_Sort sunt doi dintre cei mai importanti algoritmi de sortare. Acestia vor fi prezentati ca studii de caz la metoda de proiectare Divide_et_impera (divide_and_conquer)
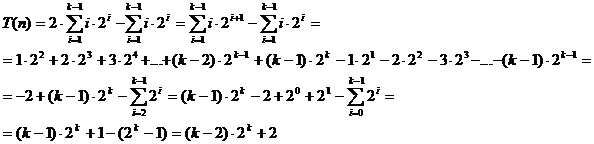
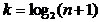