 |  |
|
In limba engleza cuvantul greedy inseamna lacom. Algoritmii de tip greedy sunt algoritmi lacomi. Ei vor sa construiasca intr-un mod cat mai rapid solutia problemei, fara a sta mult pe ganduri.
Algoritmii de tip greedy se caracterizeaza prin luarea unor decizii rapide care duc la gasirea unei solutii a problemei. Nu intotdeauna asemenea decizii rapide duc la o solutie optima, dar vom vedea ca exista anumite tipuri de probleme unde se pot obtine solutii optime sau foarte apropiate de optim.
Algoritmii de tip Greedy se aplica la acele probleme unde datele de intrare sunt organizate sub forma unei multimi A si se cere gasirea unei submultimi B A care sa indeplineasca anumite conditii astfel incat sa fie acceptata ca solutie posibila.
In general pot sa existe mai multe submultimi B A care sa reprezinte solutii posibile ale problemei. Dintre toate aceste submultimi B se pot selecta, conform unui anumit criteriu, anumite submultimi B* care reprezinta solutii optime ale problemei. Scopul este de a gasi, daca este posibil, una din multimile B*. Daca acest lucru nu este posibil, atunci scopul este gasirea unei multimi B care sa fie cat mai aproape de multimile B*, conform criteriului de optimalitate impus.
Construirea multimii B se face printr-un sir de decizii. Initial se porneste cu multimea vida (B = Ø). Fiecare decizie consta in alegerea unui element din multimea A, analiza lui si eventual introducerea lui in multimea B. In functie de modul in care se iau aceste decizii, multimea B se va apropia mai mult sau mai putin de solutia optima B*. In cazul ideal vom avea B = B*.
Algoritmii de tip greedy nu urmaresc sa determine toate solutiile posibile si sa aleaga dintre ele, conform criteriului de optimalitate impus, solutiile optime. Dupa cum spune si numele, algoritmii de tip greedy sunt caracterizati prin lacomie si nu au rabdarea sa investigheze toate variantele posibile de alegere a solutiei. Ei incep construirea unei solutii pornind de la multimea vida, apoi lucreaza in pasi, intr-un mod cat se poate de hotarat: la fiecare pas se ia cate o decizie si se extinde solutia cu cate un element.
La fiecare pas se analizeaza cate un element din multimea A si se decide daca sa fie sau nu inclus in multimea B care se construieste. Astfel se progreseaza de la Ø cu un sir de multimi intermediare (Ø, B0, B1, B2, ), pana cand se obtine o solutie finala B.
Ca si schema generala de lucru, exista doua variante de implementare a algoritmilor de tip Greedy.
Prima varianta foloseste doua functii caracteristice: alege si posibil. alege este o functie care are rolul de a selecta urmatorul element din multimea A care sa fie prelucrat. Functia posibil verifica daca un element poate fi adaugat solutiei intermediare Bi astfel incat noua solutie Bi+1 care s-ar obtine sa fie o solutie valida. Prezentam in continuare pseudocodul pentru aceasta prima varianta greedy. Se considera ca numarul de elemente al multimii A este n.
B = multimea vida
for (i=0; i<n; i++)
Dificultatea la aceasta prima varianta consta in scrierea functiei alege. Daca functia alege este bine conceputa, atunci putem fi siguri ca solutia B gasita este o solutie optima. Daca functia alege nu este foarte bine conceputa, atunci solutia B gasita va fi doar o solutie posibila si nu va fi optima. Ea se poate apropia insa mai mult sau mai putin de solutia optima B*, in functie de criteriul de selectie implementat.
A doua varianta de implementare difera de prima prin faptul ca face o etapa initiala de prelucrare a multimii A. Practic se face o sortare a elementelor multimii A, conform unui anumit criteriu. Dupa sortare, elementele vor fi prelucrate direct in ordirea rezultata. Prezentam in continuare pseudocodul pentru aceasta a doua varianta greedy.
B = multimea vida
prelucreaza(A)
for (i=0; i<n; i++)
La a doua varianta, dificultatea functiei alege nu a disparut, ci s-a transferat functiei prelucreaza. Daca prelucrarea multimii A este bine facuta, atunci se va ajunge in mod sigur la o solutie optima. Altfel se va obtine doar o solutie posibila, mai mult sau mai putin apropiata de optim.
Enunt Se condidera n orase. Se cunosc distantele dintre oricare doua orase. Un comis-voiajor trebuie sa treaca prin toate cele n orase. Se cere sa se determine un drum care porneste dintr-un oras, trece exact o data prin fiecare din celelalte orase si apoi revine la primul oras, astfel incat lungimea drumului sa fie minima.
Rezolvare Pentru gasirea unei solutii optime la aceasta problema este nevoie de algoritmi cu timp de rulare foarte mare (de ordin exponential O(2n)). In situatiile practice asemenea algoritmi cu timp foarte mare de rulare nu sunt acceptabili. Ca urmare se face un compromis si se accepta algoritmi care nu gasesc solutia optima ci doar o solutie aproape de optim, dar au in schimb un timp de rulare mic. Propunem in continuare o solutie greedy la aceasta problema. Ideea este urmatoarea. Se porneste dintr-un oras oarecare. Se cauta drumul cel mai scurt care pleaca din orasul respectiv catre orase nevizitate inca. Se parcurge acel drum si se ajunge intr-un alt oras. Aici din nou se cauta cel mai scurt drum catre orasele nevizitate inca. Se parcurge si acest drum, ajungandu-se intr-un nou oras. Repetand acesti pasi se parcurg toate orasele. La final se parcurge drumul care duce inapoi spre primul oras.
Sa consideram exemplul din figura 1. Avem 4 orase cu distantele reprezentate in figura.
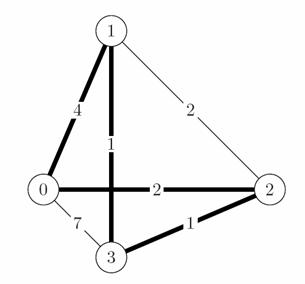
Figura 1: Retea de orase pentru problema comis-voiajorului
Pornim vizitarea oraselor din orasul 0. De aici alegem drumul cel mai scurt catre orasele nevizitate, si anume (0,2) de lungime 2. Ajunsi in orasul 2, alegem din nou drumul cel mai scurt spre orasele nevizitate, si anume (2,3) de lungime 1. Din orasul 3 mai avem doar un singur oras nevizitat, 1, asa ca alegem drumul spre el (3,1) de lungime 1. In acest moment am parcurs toate orasele si ne reintoarcem in orasul 0 pe drumul (1,0) de lungime 4. Drumul rezultat este 0, 2, 3, 1, 0, iar distanta totala de parcurs este 2 + 1 + 1 + 4 = 8.
Implementare Distantele intre orase le memoram intr-un tablou bidimensional D. Distanta intre orasele (i,j) va fi memorata in elementul di,j al matricii. In termeni Greedy, multimea initiala A este multimea tuturor perechilor de orase. Pentru reteaua de orase din figura 2 multimea A contine elementele . Multimea B care trebuie gasita va contine o parte din aceste perechi de orase, si anume acele perechi care inlantuite sa formeze un drum ce trece prin toate orasele. Daca avem un numar de n orase, atunci multimea B va contine n perechi de orase.
In implementare nu vom lucra cu multimea A sub aceasta forma explicita de perechi de orase, ci vom folosi matricea distantelor D. De asemenea drumul comis-voiajorului nu il vom pastra sub forma de perechi de orase, ci sub forma unui sir al oraselor.
Pentru a memora drumul parcurs de comis-voiajor, folosim un tablou unidimensional drum. In acest tablou vom memora indicii oraselor parcuse, in ordinea parcurgerii.
Pentru a sti care orase au fost parcurse, facem o marcare logica a oraselor folosind un tablou unidimensional vizitat. Elementele din acest tablou care au valoarea 1 reprezinta orase vizitate.
Cod sursa In continuare este prezentat codul sursa in limbajul C care implementeaza algoritmul descris mai sus.
#include <stdio.h>
/* Numarul maxim de orase. */
#define N_MAX 30
/* Constanta care se foloseste ca valoare
de initializare la cautarea minimului. */
#define MINIM 10000
/* Numarul de orase. */
int n;
/* Matricea distantelor dintre orase. */
int d[N_MAX][N_MAX];
/* Drumul comis voiajorului. Contine
indicii oraselor in ordinea in care
sunt ele parcurse. */
int drum[N_MAX];
/* Vector care memoreaza care orase au
fost vizitate. vizitat[k] va fi 1 daca
orasul k a fost vizitat, 0 altfel. */
int vizitat[N_MAX];
/* Functie care alege urmatorul element care
sa fie prelucrat din multimea oraselor.
Primeste ca parametru ultimul oras care
a fost vizitat, si returneaza urmatorul
oras care sa fie vizitat precum si lungimea
drumului catre acesta. */
void alege(int ultimul, int *min, int *j_min)
}
int main(void)
/* Citim datele din fisier. */
fscanf(fin, '%d', &n);
for (i=0; i<n; i++)
for (j=0; j<n; j++)
fscanf(fin, '%d', &(d[i][j]));
/* Afisam pe ecran datele preluate din fisier. */
printf('Avem %d orase.n', n);
printf('Distantele dintre orase sunt:n');
for (i=0; i<n; i++)
printf('n');
/* Initial nici un oras nu este vizitat. */
for (i=0; i<n; i++)
vizitat[i] = 0;
/* Primul oras vizitat este cel cu numarul '0'.
Costul total este zero deocamdata. */
drum[0] = 0;
vizitat[0] = 1;
count = 1;
cost = 0;
/* Parcurgem restul de n-1 orase. */
for (i=0; i<n-1; i++)
/* Parcurgem drumul de la ultimul oras vizitat
catre primul oras si actualizam costul
total. */
cost += d[drum[n-1]][0];
/* Afisam drumul parcurs. */
printf('nDrumul are costul %d si este:n', cost);
for (i=0; i<n; i++)
printf('%d ', drum[i]);
printf('0n');
return 0;
Fisierul cu date de intrare pentru reteaua de orase din figura 1 este urmatorul:
Imbunatatiri Algoritmul greedy prezentat se poate imbunatati pentru a furniza solutii mai aproape de solutia optima. O varianta de imbunatatire este sa nu se porneasca doar din primul oras la parcurgerea drumului. Se poate relua calculul avand ca punct de pornire fiecare oras pe rand si se poate memora minimul global astfel obtinut.
Metoda de rezolvare Divide and Conquer se poate aplica la problemele care se pot descompune in subprobleme de aceeasi natura cu problema principala, dar de dimensiuni mai mici.
La unele probleme aceasta posibilitate de descompunere in subprobleme de acelasi tip este evidenta. Vom vedea insa ca sunt si probleme unde o asemenea descompunere nu apare de la prima vedere.
Se poate pune intrebarea "cum rezolvam subproblemele?". Raspunsul este: "in acelasi mod in care am rezolvat problema principala". Metoda Divide and Conquer se preteaza foarte bine la implementari recursive. Din moment ce stim sa impartim problema principala in subprobleme, ce ne opreste sa facem acelasi lucru cu fiecare subproblema in parte? Putem imparti fiecare subproblema in subsubprobleme, pe care la randul lor le impartim in subsubsubprobleme, s.a.m.d.
Cand ne oprim cu aceste impartiri recursive? Atunci cand ajungem la subprobleme de dimensiuni atat de mici incat rezolvarea lor este triviala.
In general implementarea metodei Divide and Conquer se face prin functii recursive. De regula vom avea o singura functie care primeste ca parametri informatiile necesare pentru a rezolva o subproblema si returneaza rezultatele pentru subproblema respectiva.
Functia va determina daca subproblema este una triviala, caz in care va calcula direct solutia pentru ea. Daca subproblema nu este una triviala, atunci functia va imparti subproblema in subsubprobleme si se va auto-apela in mod recursiv pentru fiecare din ele. Pe urma va combina rezultate obtinute pentru subsubprobleme si va gasi solutia pentru subproblema.
Prezentam schema generala de lucru a unei asemena functii, in pseudocod:
function divide(* parametri care definesc o subproblema)
else
Pentru a rezolva problema principala, tot ce trebuie facut este sa se apeleze functia recursiva cu acei parametri care definesc problema principala.
Enunt Fie trei tije notate cu a, b si c. Pe tija a se afla n discuri de dimensiuni diferite, asezate in ordinea descrescatoare a diametrelor, astfel incat discul cu diametrul cel mai mare se afla cel mai jos, iar discul cu diametrul cel mai mic se afla in varful stivei. Sa se gaseasca o modalitate de a muta toate cele n discuri de pe tija a pe tija b, folosind tija intermediara c, atfel incat in final discurile sa fie ordonate tot descrescator. In timpul operatiilor care se fac, este interzisa plasarea unui disc mai mare peste un disc mai mic.
Rezolvare Problema noastra initiala este sa mutam n discuri de pe tija a pe tija b, folosind tija intermediara c. O putem codifica in felul urmator: (n,a,b,c). Daca am gasi o modalitate de a muta n-1 discuri de pe tija a pe tija intermediara c, atunci am putea sa mutam discul cel mai mare de pe tija a pe tija b. Pe urma ar trebui sa aducem cele n-1 discuri de pe tija c pe tija b si problema ar fi rezolvata. Pentru a muta n-1 discuri de pe tija a pe tija c, putem folosi ca tija intermediara tija b. La fel, pentru a muta inapoi cele n-1 discuri de pe tija c pe tija b, putem folosi ca tija intermediara tija a.
Putem reformula cele zise mai sus in felul urmator: problema (n,a,b,c) se rezuma la problema (n-1,a,c,b), urmata de mutarea discului de diametru maxim de pe a pe b, urmata de problema (n-1,c,b,a).
Implementare Implementarea se face printr-o functie recursiva. Functia primeste patru parametri: numarul de discuri de pe tija initiala, tija initiala, tija finala si tija intermediara. Se descompune problema in subprobleme, in modul descris mai sus. Cazul trivial este acela cand avem de mutat un singur disc si in aceasta situatie discul este mutat direct.
Cod sursa Prezentam in continuare codul sursa in limbajul C care rezolva problema:
#include <stdio.h>
/* Functie care muta n discuri de pe tija initiala
pe tija finala, folosind o tija intermediara.
Rezolvarea se face in maniera Divide and Conquer. */
void hanoi(int n, char t_initial, char t_final,
char t_intermediar)
/* Daca avem un singur disc de mutat, atunci
il mutam direct. La acest nivel problema are
o rezolvare triviala. */
else
int main(void)
Enunt Se da un sir de n numere reale . Sa se determine valoarea minima si valoarea maxima din acest sir de numere.
Rezolvare Metoda imediata de rezolvare este parcurgerea intregului sir si inspectarea fiecarui element de doua ori, o data pentru aflarea minimului si a doua oara pentru aflarea maximului. Codul sursa in limbajul C pentru aceasta metoda imediata este:
#include <stdio.h>
/* Declaram sirul de numere direct din cod. Alternativ
el poate fi citit de la tastatura sau din fisier. */
#define N 10
int x[] = ;
int main(void)
/* Afisam rezultatele. */
printf('Minimul este %d.n', min);
printf('Maximul este %d.n', max);
printf('Comparatii facute: %d.n', comp);
return 0;
Daca analizam metoda de mai sus, vom vedea ca ea face comparatii inutile, deoarece orice element care este candidat pentru minim nu poate fi in acelasi timp candidat pentru maxim, si invers. Deci este redundant sa testam fiecare element in parte atat pentru minim cat si pentru maxim.
Putem aplica tehnica Divide and Conquer, impartind sirul de numere in doua parti. Determinam minimul si maximul pentru fiecare din cele doua parti, iar pe urma determinam maximul global prin compararea celor doua maxime partiale, iar minimul global prin compararea celor doua minime partiale.
Implementare Pentru implementare vom defini o functie recursiva ce va cauta minimul si maximul intr-o secventa a sirului. Initial vom apela aceasta functie pentru intregul sir. Functia se va apela pe ea insasi, recursiv, pentru jumatarea stanga si pentru jumatatea dreapta a secventei.
Cod sursa Prezentam in continuare codul sursa in limbajul C pentru rezolvarea problemei.
#include <stdio.h>
/* Declaram sirul de numere direct din cod. Alternativ
el poate fi citit de la tastatura sau din fisier. */
#define N 10
int x[] = ;
/* Numaram cate comparatii se fac in total. */
int comp = 0;
/* Functie care determina minimul si maximul dintr-o
secventa a sirului de numere. Secventa este
delimitata de indicii 'st' si 'dr'. Valorile minime
si maxime gasite vor fi returnate prin pointerii
'min' si 'max' primiti ca si parametru. */
void minmax(int st, int dr, int *min, int *max)
/* Daca secventa contine doua numere, atunci
facem o comparatie pentru a gasi minimul si
maximul. */
else if (st == dr - 1)
else
}
/* Daca avem mai multe numere, atunci divizam
problema in subprobleme. */
else
int main(void)
Daca rulam in paralel cele doua programe, vom vedea ca intradevar pentru acelasi sir de numere metoda Divide and Conquer face mai putine comparatii decat metoda clasica.
Enunt Se considera n orase. Pentru diferite perechi de orase (i, j), 0<i<n, 0<j<n se cunoaste costul conectarii lor directe ci,j. Nu toate perechile de orase pot fi conectate; pentru perechile care nu pot fi conectate nu se precizeaza costul. Se cere sa se construiasca o retea prin care oricare doua orase sa fie conectate intre ele direct sau indirect si costul total al conectarii sa fie minim.
Rezolvare Se poate arata ca reteaua de conectare ceruta este un arbore. Problema mai este cunoscuta si ca problema determinarii arborelui partial de cost minim intr-un graf. Pentru aceasta problema exista un algoritm greedy de rezolvare numit algoritmul lui Prim. In literatura de specialitate exista argumentarea matematica a faptului ca acest algoritm gaseste intotdeauna solutia optima de conectare a oraselor.
Se construieste arborele partial minim in maniera greedy, adaugand cate un nod la fiecare pas. La inceput de tot arborele partial este vid, nu contine nici un nod. Primul pas consta in adaugarea unui nod arbitrar in arbore. Pe urma, la fiecare pas se cauta muchia de cost minim care porneste dintr-un nod deja adaugat la arbore si ajunge intr-un nod care nu este in arbore. Se adauga in arbore nodul in care sfarseste muchia gasita.
Sa consideram spre exemplu o retea de 7 orase numerotate de la 0 la 6. Costurile de conectare a oraselor sunt redate in figura 2.
Figura 2: Costuri de conectare a oraselor pentru problema conectarii oraselor cu cost minim
Arborele minim este redat cu linii ingrosate. El a fost construit pas cu pas, conform procedeului descris mai sus. Initial arborele a fost vid. La primul pas s-a adaugat un nod arbitrar, si anume nodul 0.
Pe urma s-a ales muchia de cost minim care pleaca din nodul 0 catre celelalte noduri. Muchia de cost minim a fost (0,2) de cost 10. Nodul 2 a fost adaugat in arbore.
La urmatorul pas s-a ales muchia de cost minim care pleaca din nodurile 0 sau 2 catre celelalte noduri. Muchia aleasa a fost (2,1) de cost 9. Nodul 1 a fost adaugat in arbore.
La urmatorul pas s-a ales muchia de cost minim care pleaca din nodurile 0, 2 sau 1 catre nodurile inca neintroduse in arbore. Muchia aleasa a fost (1,5) de cost 3. Nodul 5 a fost adaugat in arbore.
Urmatoarea muchie aleasa a fost (5,4) de cost 2. Nodul 4 a fost adaugat in arbore. Apoi a fost aleasa muchia (4,6) de cost 2 si nodul 6 a fost adaugat si el in arbore.
Pe urma a fost aleasa muchia (1,3) de cost 4 si nodul 3 a fost introdus in arbore. In acest moment algoritmul s-a incheiat deoarece toate orasele au fost conectate la retea. Costul total al conectarii a fost 10 + 9 + 3 + 2 + 2 + 4 = 30.
Implementare Matricea costurilor, C, se retine intr-un tablou bidimensional. Pentru perechile de orase intre care nu se poate face legatura se va trece in matricea costurilor valoarea 0. In termeni Greedy, multimea noastra initiala de elemente A este mutimea tuturor perechilor de orase intre care se poate stabili legatura directa. Adica A=. Pentru graful din figura 1, multimea A va contine elementele .
Submultimea B pe care o cautam va contine o parte din perechile aflate in multimea A. Se poate demonstra ca solutia optima B* contine n-1 perechi atunci cand numarul de orase este n (presupunem ca graful este conex, adica se poate construi o retea care sa conecteze toate orasele).
Pentru construirea multimii B, vom selecta orasele rand pe rand pentru a le adauga la retea. Vom spune ca un oras este selectat atunci cand el a fost conectat la reteaua de orase printr-o muchie care face parte din multimea B.
In implementare nu vom lucra cu multimea A sub forma explicita de perechi, ci vom folosi matricea costurilor C. Vom eticheta liniile si coloanele matricei costurilor dupa cum urmeaza. Atunci cand un oras oi este selectat, linia i din matrice se marcheaza, iar coloana i din matrice se sterge.
Pentru a alege urmatorul element din multimea A care sa fie prelucrat, cautam cel mai mic cost din matricea costurilor din liniile marcate si coloanele care nu sunt sterse. Sa zicem ca cel mai mic cost a fost gasit ca fiind elementul ci_min,j_min. Atunci urmatorul element din multimea A care va fi prelucrat este perechea (i_min,j_min).
Stergerea coloanelor din matricea costurilor nu va insemna o stergere fizica, ci doar una logica. Vom folosi doi vectori prin care vom memora care linii sunt marcate si care coloane sunt sterse.
O schema de cod sursa pentru rezolvarea acestei probleme arata astfel:
/* Numarul maxim de noduri din graf. */
#define N_MAX 30
/* Numarul de orase. */
int n;
/* Matricea costurilor de conectare a oraselor. */
int c[N_MAX][N_MAX];
/* Vector care indica liniile marcate din matricea
costurilor. marcat[k] va fi 1 pentru liniile
marcate si 0 pentru liniile nemarcate. */
int marcat[N_MAX];
/* Vector care indica coloanele sterse din matricea
costurilor. sters[k] va fi 1 pentru coloanele
sterse si 0 pentru coloanele nesterse. */
int sters[N_MAX];
/* Functie care alege urmatorul element care sa
fie prelucrat din multimea A, adica o pereche
de orase intre care sa se construiasca drum.
Se parcurg liniile marcate si coloanele
nesterse din matricea costurilor si se
alege costul minim.
Se returneaza costul minim gasit, si linia si
coloana unde apare el. */
void alege(int* min, int *i_min, int* j_min)
int main(void)
/* Afisam arborele partial minim pe care l-am gasit. */
return 0;
Fisierul cu date de intrare pentru graful din figura 2 este urmatorul:
Se dau N puncte in plan, situate pe o dreapta paralela cu axa OX. Sa se determine perechea de puncte care sunt cel mai apropiate unul de altul. Daca exista mai multe asemenea perechi, se va determina una din ele.
Datele de intrare se citesc din fisierul "puncte.in". Pe prima linie din fisier apare N, numarul de puncte. Pe a doua linie apar N valori reale, reprezentand coordonatele X ale celor N puncte. Coordonatele Y ale punctelor nu se precizeaza, deoarece toate punctele au aceeasi coordonata Y. In fisier punctele apar sortate crescator in ordinea coordonatei X.
Programul va scrie in fisierul "puncte.out" doua valori reale reprezentand coordonatele celor mai apropiate doua puncte.
Rezolvarea divide and conquer se face in felul urmator:
se imparte multimea de puncte in doua jumatati;
punctele fiind sortate dupa coordonata X, avem trei variante posibile:
fie perechea pe care o cautam se afla in prima jumatate;
fie perechea se afla in a doua jumatate;
fie un punct al perechii se afla in prima jumatate si celalalt punct in a doua jumatate;
in maniera divide and conquer rezolvam subproblemele pentru cele doua jumatati;
memoram distanta minima gasita pentru prima jumatate si pentru a doua jumatate;
verificam daca exista o pereche de puncte cu un punct din prima jumatate si un punct din a doua jumatate astfel incat sa obtinem o distanta mai mica:
se poate demonstra faptul ca singura varianta in care am putea obtine o distanta mai mica este folosind cel mai din dreapta punct din prima jumatate impreuna cu cel mai din stanga punct din a doua jumatate;
in final pastram distanta cea mai scurta din cele trei variante.
Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre: |
| Copyright © 2024 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |