Metoda Backtracking

Descrierea Metodei

Metoda BackTracking se aplica in probleme de cautare. Metoda este adecvata problemelor in care solutia se poate exprima ca un n-uplu (x₁ x₂ x_n) , x_i S_i - finita , i = 1,n . Solutia trebuie sa satisfaca sau sa minimizeze / maximizeze o functie criteriu P(x₁ x₂ x_n). Uneori se solicita toate solutiile.Daca |S₁| = m₁ , |S₂| = m₂ . . . |S_n| = m_n , atunci numarul total de n-uple este m=m₁ m₂ m_n. Metoda nu asigura ca nu se vor incerca toate cele m posibilitati , dar practic reduce mult numarul de n-uple care se incearca prin folosirea functiei criteriu. Ideea este de a folosi o forma partiala a functiei criteriu P_i(x₁ x₂ x_i) care elimina familii intregi de n-uple. Daca de exemplu solutia partiala (x₁ x₂ x_i) nu are nici o sansa de a conduce la o solutie completa , toate cele m_i+1 m_i+2 m_n n-uple cu (x₁ x₂ x_i) pe primele i pozitii se abandoneaza.

Spatiul solutiilor. Restrictii.

S₁ S₂ S_n se numeste spatiul solutiilor problemei, iar restrictiile de forma (x₁,x₂,,x_n) S₁ S₂ S_n se numesc restrictii explicite ; restrictiile (x₁, x₂ ,,x_n) satisfacind P se numesc restrictii implicite

Exemplu 1: Problema celor 8 dame pe tabla de sah : Data fiind S==multimea celor 8 dame si o tabla de sah ( 8 linii si 8 coloane) sa se plaseze cele 8 dame asfel incit sa nu existe doua dame pe aceeasi linie, coloana sau diagonala.

O solutie poate fi exprimata printr-un 8-uplu X=(x₁,x₂,.x₈) unde x_i = coloana pe care se plaseaza dama I ( linia pe care se plaseaza dama I este i )

- Deoarece S_i = S, i=1, . ,8 rezulta ca spatiul de solutii S S S S are 8⁸ 8-uple;

de 8ori

- Restrictia explicita: 1 x_i 8 , i=1, . ,8

- Restrictii implicite -o singura dama pe o coloana : x_i x_j , ( ) i j, i,j=1, . ,8

-o singura dama pe o diagonala : |i-j| |x_i-x_j| , ( ) i j, i,j=1, . ,8

Exemplu 2: Submultimi de suma data : Date fiind S=, w_i 0 1 i n si M-o valoare M > 0, sa se determine toate submultimile S' S, S`= cu proprietatea x₁+x₂++x_k=M

Cazul n=4 S= M=31 S=(11,13,24,7); solutii : X₁=(11,13,7), X₂=(24,7) sau exprimate prin indicii i ai elementelor w_i I S, X₁=(1,2,4), X₂=(3,4)

Pentru cazul exprimarii solutiilor prin indicii i ai elementelor w_i I S restrictiile sint urmatoarele:

- Restrictii explicite 1 x_i n, , i=1, . ,n

- Restrictii implicite: x_i x_j si =M

x_i<x_i+1 pentru a evita generarea aceleasi multimi

ex.:=

O alta abordare: X=(x₁,x₂,..x_n), x_i = 0 sau 1; = M

Spatiul solutiilor este de dimensiune 2ⁿ.

Organizarea sub forma de arbore a spatiului solutiilor

Metoda backtracking rezolva o problema prin cautarea sistematica a solutiei in spatiul solutiilor. Conceptual , aceasta cautare foloseste o organizare a spatiului solutiilor sub forma unui arbore.

Exemplul 1 : Problema celor n-dame

folosim n=4

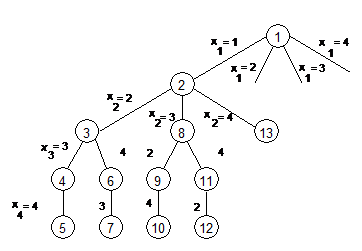
In acest arbore arcele de la nivel i la i+1 sint etichetate cu valori x_i.

Spatiul solutiilor = secventele de etichete de la radacina la nodurile frunza.Nodurile sint etichetate in

sensul parcurgerii depth-first.

Exemplul 2: Submultimi de suma data (11,13,24,7) M=31

Traversare breadth-first.

Notiuni :

-starea problemei - fiecare nod intr-un arbore defineste o stare a problemei;

-spatiul starilor - toate drumurile de la radacina la noduri;

-stari solutie - acele stari (noduri) pentru care drum de la radacina la nod etichetat cu un n-uplu;

-stari raspuns - stari care satisfac conditiile implicite P;

-arborele spatiului starilor - spatiul starilor problemei organizat sub forma de arbore.

Arborii construiti astfel sint arbori statici si nu depind de instanta problemei. Exista arbori dinamici care depind de problema. Un exemplu ar fi cazul in care functie de valoarea lui x₁ se decide daca la primul nivel este x₁ sau x₂ s.a.m.d.

Backtracking si Branch-and-Bound

Exista doua strategii de generare a nodurilor corespunzatoare starilor problemei : depth-first si breadth-first.

Nodurile se clasifica in:

-nod viu -nod generat pentru care nu s-au generat descendenti;

-E-noduri -noduri in expandare - noduri vii pentru care procesul de generare al

descendentilor este in curs;

-noduri moarte -nod generat care nu are descendenti (si nici nu va avea) sau pentru care toti descendentii s-au generat.

In strategia depth-first, pentru E-nodul curent se identifica un descendent C care devine noul E-nod si procesul se aplica recursiv.

In strategia breadth-first, pentru E-nodul curent se genereaza toti descendentii si se trec in lista de noduri vii sau moarte.

In ambele strategii in orice moment se aplica functia criteriu (restrictiile implicite), numita si functia de marginire care seteaza un nod ca nod mort fara a-i mai genera descendentii.

Prima tehnica este numita backtracking

A doua tehnica este numita Branch-and-Bound

Exemplu pentru tehnica backtracking: Problema celor 4 dame:

Ordinea de generare este:

Modelul metodei

Fie (x₁,x₂,x_i) un drum de la radacina la un nod intr-un arbore spatiu de stari.

Fie T(x₁,x₂,..x_i) multimea tuturor valorilor posibile pentru x_i+1 astfel incit

(x₁,x₂,..x_i,x_i+1) este de asemenea un drum de la radacina la un nod.

Fie B_i+1(x₁,x₂,..x_i+1) functia (predicatul) de marginire derivat din P - functia criteriu

B_i+1(x₁,x₂,..x_i+1) = false daca x_i+1 este nod mort, de blocaj;

true daca x_i+1 se extinde;

Backtrack-iterativ (n)

Solutile sint generate in x[1,2,n];

// T(x₁,..x_k-1)=

// B_k(x₁, x_k) - functie (predicat) de marginire;

else

k=k-1 ;

}

backtrack-recursiv (k)

// Solutile sint generate in x[1,2,n];

//T(x₁,..x_k-1)=

//B_k(x₁, x_k) - functie (predicat) de marginire;

for (each x_k a.i. x_k= y I T(x₁.x_k-1)

and B_k(x₁..x_k-1,x_k)=true

Observatii

1.Eficienta algoritmului depinde de

- timpul pentru generarea urmatorului x_k;

- numarul de elemente din T(x₁..x_k-1)

- functia de marginire B;

- numarul total de noduri.

2.Pentru multe probleme, multimile S_i, se pot lucra in orice ordine, iar elementele din T(x₁,x_k-1) la fel.

Folosind aceasta observatie se pot stabili anumite euristici - strategii de organizare a elementelor lui S_i cu scopul de a reduce nivelul de backtraking.

3.Ordinul de complexitate este O(2ⁿ) sau O(n!)

Metoda insa rezolva , de obicei, mult mai rapid problemele fara insa a se sti exact cit de repede.

Uneori se poate incerca o estimare a timpului backtrcking si aceasta pornind de la o estimare a numarului de noduri.

Estimarea numarului de noduri se poate face prin urmatoarea procedura generala:

estimate ( )

if(|T_k|=0) break;

r=r |T_k| ;

nr=nr+r ;

x_k=random-choose(T_k);

k=k+1;

}

return (nr)

Studii de caz

Problema celor 8 dame

Daca se considera 2 elemente pe aceeasi diagonala (i,j) ,(k,l)

i-j=k-l sau i+j=k+l

j-l=i-k j-l=k-i

adica se poate folosi conditia |j-l|=|k-i|.

Construim functia place(k) care returneaza true daca dama cu numarul de ordine k poate fi plasata pe coloana data de x[k].

Operatiile care se fac sint:

- se testeaza daca x[k] x[i] i=1,2, . ,k-1

- se testeaza daca nu alta dama in aceeasi diagonala.

Functia place lucreaza in O(k-1)

place(k)

return true

n_queen (n)

}

else

k=k-1; // x[k] > n backtrack

}

}

Submultimi de suma data

Fie n numere pozitive S = w_i> w_i w_j i j si M>

Sa se determine toate submultimile S` S cu 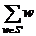=M

Folosim notatia solutiei sub forma X= x_i=0 sau 1

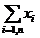w_i=M

Arborele spatiului starilor va fi de forma:

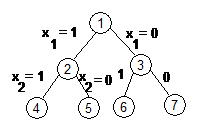
Consideram w₁,w₂.w_n in ordine crescatoare (fara a fi o restrictie generala)

Functia de marginire

B_k(x₁,x₂,.x_k) = true if (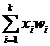 + 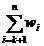M and 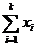w_i + w_k+1 M)

w_i-cresc.

= false - altfel

SumSubset(s,k,r)

}

return

Observatie:

Functia intra in executie ,avind asigurate conditiile B_k-1=true : s+w_k M si s+r M.

Initial w₁ M si 0+ M corespunzind apelului SumSubset (0,1,)

Aceste conditii sunt asigurate la apelul recursiv.

Nu se verifica explicit k>n deoarece initial s = 0 < M si s+r M. Rezulta r 0 deci k nu poate depasi n. De asemenea in linia XXX deoarece s+w_k < M si s+r M rezulta r w_k, deci k+1 n.