TEORIA
FOTOELASTICITATII
LEGİLE ELASTİCİTĀTİİ
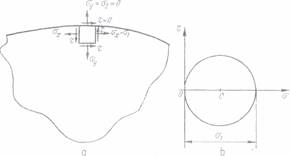
Determinarea starii de tensiune dintr-o piesa cu ajutorul
fotoelasticitatii se bazeaza pe aparitia fenomenului de birefrigerenta
accidentala la materialele transparente,atunci cand
sunt supuse unei stari de tensiune.In stare netensionata materialul este izotrop din punct de vedere optic, prezentind
in toate directiile acelasi indice de refraetie n0. Daca modelul este solicitat de un sistem de
forte exterioare, va lua nastere o stare de tensiune care face ca
materialul sa devina birefrigerent
si sa-si modifice proprietatile optice Acest
f enomen este cunoscut sub demimirea de legea
calitativa a
calitatii. Notind cu n si n2 indicii de refractie
in lungul directiilor
principale si cu no indicele de
refractive al materialului in stare netensionata,Maxwell
a stabilit relatia de legatura intre starea de tensine din model si efectul
optic produs de aceasta
 (1.)
(1.)
Relatiile 1. sunt cunoscute
sub denumirea de legea cantitativa a fotoelasticitatii sau legea efortului
optic.Coeficientii C1 si C2 din aceste relatii se numesc coeficienti de
efort optic.Scazand cele doua relatii obtinem cea de a doua forma a legii
efortului fizic:
 ( )
( )
Unde
Cσ=C1+C2=coeficient de efort optic relativ
3. CONSTANTA FOTOELASTİCĀ
Dupa cum s-a
vazut la polariscopul circular aranjat pentru camp intunecat,extinctia totala se obtine atunci cand este satisfacuta
relatia
δ=kλ,k=ordinul de banda al franjei
Comparand aceasta relatie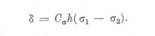 cu cea scrisa anterior se obtine :
cu cea scrisa anterior se obtine : 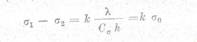
Unde σo=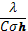 =constanta fotoelastica a
modelului=daN/ cm2
. franja
=constanta fotoelastica a
modelului=daN/ cm2
. franja
Din
expresia (45) rezulta ca diferenta tensiunilor principale σ1- σ2=
=2τmax
intr-un punct din model, poate fi determinata cu usurinta daca se cunoaste ordinul de banda al
franjei din punctul respectiv si constanta fotoelastica a modelului.
Figura 15
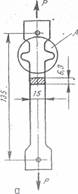
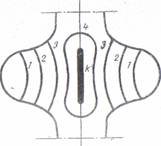 Detaliul A
Detaliul A
epruvetei. Incarcarea trebuie astfel realizata
incit sa se asigure o centrare cit mai buna a sarcinii aplicate. In acest caz izocromatele produse in zona prevazuta cu umflatura sint simetrice fata de axa epruvetei (fie. 15. b).
b)etalonarea la incovoiere pura
Este metoda cea mai utilizata pentru
etalonarea materialelor fotoelastice cu sensibilitate optica medie si
ridicata.Forma epruvetei cat si dispozitivul pentru realizarea solicitarii de
incovoiere pura sunt prezentate in figura Pe portiunea de bara solicitata la incovoiere
pura, izocromatele apar
sub forma unor linii paralele echidistante de o parte si de alta a axei epruvetei (fig. 18). Franjele
paralele si echidistante arata ca repar-
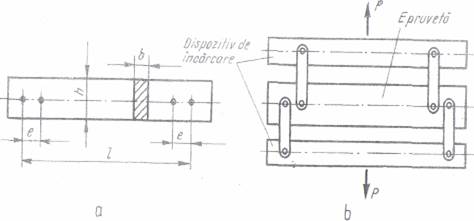
Fig. 17.
2 3 4 5 6 Fig. 16.
tizarea tensiunilor este aceeasi in toate sectiunile, iar intr-o sectiune tensiunile au o variabla liniara data
de formula lui Navier. Tensiunea
maxima diu epruveta este:
σmax= =
=
 (c)
(c)
Tinind seama de (45), rezulta
max=kσ (d)
Comparand relatiile (c) si (d) se obtine:
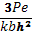
Incarcarea epruvetei trebuie sa se faca in acest caz
astfel ca izocromata de un anumit ordin k, sa fie tangenta la contur
(atit la partea superioara
cit si la cea
inferioara). In fig. 18 se arata modul de notare si distributia tensiunilor in sectiune.
 Fig. 18.
Fig. 18.
c) Etalonarea cu disc comprimat axial Metodele de etalonare prezentate mai sus se refera la starea de
tensiune dupa o singura directie. Etalonarea fotoelastica
se poate face si in cazul starii plane de tensiune folosind un
disc comprimat diametral. Tensiunile principale in centrul discului, cunoscute
din teoria elasticitatii, sint:
σ1= si σ2=-
si σ2=- 
unde P este sarcina, D diametrul
discului si t grosimea (fig. 19, a). Cu ajutorul expresiilor (e) poate fi calculata diferenta
σ1- σ2, Variind incarcarea P se determina proportionalitatea
dintre ordinul de banda k si ,
obt-inindu-se astfel curba de etalonare (fig. 19, b).
INREGISTRAREA DATELOR FOTOELASTICE
1. İNREGİSTRAREA
İZOCLİNELOR
Izoclinele obtinute in polariscopul cu
lumina polarizata plan sunt folosite pentru determinarea directiilor
tensiunilor principale in orice punct al modelulii si pentru trasarea
izostaticelor. Izoclinele de diferiti parametri, de regula
sint trasate pe hirtie sau fotografiate. Pentru obtinerea izoclinelor
dintr-un anumit interval, de exemplii de la 0° la 90°, polarizorul si
analizorul (avind axele perpendiculare), se rotesc simultan din zece in zece
grade sau din cinsprezece in cincisprezece grade, in functie de precizia impusa
determinarilor. Izoclinele obtinute prin fotografiere de
multe ori sint confuze. Fiind greu de precizat,
punctele prin care trec, in practica, se traseaza prin puncte, pe hirtie.
In acest scop pe suprafata modelului se traseaza o retea fina rectangulara, Pe
o bucata de hartie separat se deseneaza conturul modelului avand trasata
aceeasi retea de linii rectangular.O placa subtire dintr-un metal opac,avand in
mijloc o gaura cu diametrul de (1,5 . 2)mm ,se asaza pe rand cu gaura in dreptul
fiecarui nod al retelei d pe suprafata modelului.Se roteste simultan
polarizorul si analizaorul pana cand in nodul examinat se obtine extinctie
totala.Se noteaza pe hartie indreptul nodului respective unghiul cu care s-a
rotit si polarizorul continuandu-se operatia si pentru celelalte noduri.Uniind
apoi punctele de acelasi parametru se obtine spectrul izoclinelor.
Dupa cum s-a mai aratat,in
polariscopul cu lumina polarizata plan,izoclinele se suprapun peste izocromate
astel ca cele doua familii de curbe sunt greu de identificat.De aceea,pentru a
se obtine numai izoclinele se recomanda utilizarea unui model confectionat
dintr-un material cu sensibilitate optica scazuta cum este plexiglasul. Modelul
se incarca foarte putin astfel ca sa se obtina cel
mult o izocromata. Variind incarcarea, izocromata isi modifica pozitia, in timp
ce izoclinele ramin neschimbate, fiind astfel
identificate cu usurinta. In fig. 20 se prezinta cimpul
izoclinelor obtinute pentru o saiba comprimata diametral.
 Fig. 20 Din examinarea figurii 20 rezulta:
Fig. 20 Din examinarea figurii 20 rezulta:
-izoclinele
corespunzatoare tuturor parametrilor trec prin punctele izotrope A,B,C . . . .J;
-parametrul fiecarei
izocline coincide cu unghiul pe care il face cu orizontala
,tangenta dusa la contur in punctul in care izoclina intercepteaza
conturul;
-tensiunile tangentiale
fiind nule in lungul axelor verticala si orizontala,aceste
axe coincid cu directiile principale si sunt deci si izocline de parametru
zero;
tensiunile din vecinatatea
punctelor de aplicatie a sarcinii concentrate
fiind tensiuni principale, directiile principale din aceasta zona vor varia de la 00 la 180° si, prin.
urmare, izoclinele corespunzind fruturor parametrilor vor trece prin aceste puncte.
TRASAREA ZOSTAT CELOR
Avind reteaua de izocline se pot trasa
izostaticele care reprezinta traiectoriile
tensiunilor principale.Existand
doua tensiuni principale rezulta
doua familii de izostatice rectangular.Pentru trasarea traiectoriilor
tensiunilor principale se allege un sistem de axe xOy (fig. 21). Pe axa Oy se aleg o
serie de puncte P ,P , . .,Pn,la
distant egala convenabil aleasa.Prin punctul P se duce dreapta
 Fig. 21.
Fig. 21.
1 care face cu axa Ox unghiul α (identic cu parametrul izoclinei α Se noteaza cu A mijlocul
distancei dintre izoclinele 1si masurata pe
dreapta 1. Prin punctul A se duce dreapta 2 care
face cu Ox unghiul Prin mijlocul distantei dintre izoclinele si (punctul B), se
duce dreapta 3 care face cu
orizontala unghiul .
Apoi prin mijlocul distantei dintre
izoclinele si
masurata pe dreapta 3 (punctul C), se duce dreapta 4 care face cu
orizontala unghiul s.a.m.d. Infasuratoarea dreptelor 1, 2, 3, 4, este o izostatica.
Repetind aceeasi constructie, dar pornind
din
punctele P2, P3, .., Pn, se obtine o familie de
izostatice. Cealalta
familie se obtine ducind curbe ortogonale pe izostaticele trasate prin
procedeul descris mai sus.
3. INREGISTRAREA
İZOCROMATELOR
Izocromatele se inregistreaza de
regula prin fotografiere, folosind polariscopul
cu lumina polarizata circular, care asa dupa cum s-a
aratat elimina izoclinele. O problema importanta care se ridica in acest
caz este citirea
cit mai precisa a ordinului de banda. In cazul folosirii polariscopumi cu camp intunecat si cu cimp luminat se pot determina
cu precizie atit ordinele de banda intregi (1, 2, 3,.. ., k), cit si
cele fracionare( 0,5 ; 1,5 ;2,5; . 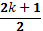
Stabilirea
ordinului izocromatelor (numerotarea), se face pornind de la punctele izotrope (singulare),care
corespund izocromatei de ordinul zero.
In absenta punctelor singulare, pentru numerotarea izocromatelor se are in vedere ca punctul de intersectie a doua
muchii perpendiculare
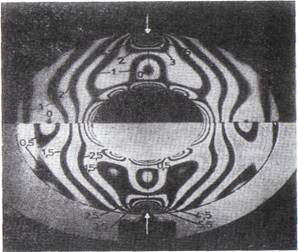 Fig. 2
Fig. 2
aflate pe un contur neincarcat, este un
punct singular. In fig. 22 se prezinta un exemplu de
numerotare a izocromatelor.
De multe ori este
necesar sa se cunoasca cu precizie ordinul de banda intr-un punct situat intre doua izocromate.
Determinarea ordinului de banda in
acest caz printr-o simpla operatie de interpolare nu este
corecta, deoarece asa cum rezulta din
(40) intensitatea luminii variaza, dupa o lege sinusoidala. In fig. 23 se prezinta variatia
intensitatii luminoa transmisa printr-o
epruveta solicitata la intindere de o sarcina progresiva observata intr-un polariscop cu lumina polarizata
circular. Diferenta intre
ordonatele punctelor situate pe curbele trasate cu linie plina se desprind
urmatoarele
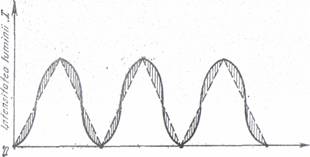
Polariscop cu camp intunecat Ordinul de banda k Fig 23
trei metode de
compensare :
a)compensarea cu epruveta de tractiune;
b)compensarea cu compensatorul Babinet-Soleil;
c)compensarea cu metoda Tardy.
Toate aceste metode de compensare necesita cunoasterea prealabila a tuturor directiilor
principale in punctul in care se citeste ordinul de banda.
COMPESAREA CU EPRUVETA DE TRACTİUNE
Functionarea compensatorului cu
epruveta de tractiuue se bazeaza pe
faptul ca o stare plana de tensiune poate fi descompusa intr-o stare de tensiune hidrostatica si o stare de tensiune
uniaxiala, asa cum rezulta din fig. 2
Dupa cum s-a aratat, starea de tensiune hidrostatica σl- σ2 = 0,
corespunde ordinului de banda zero, in timp ce starea. de
tensiune uniaxiala corespunde unei valori oarecare a ordinului de banda.
 Fig. 24
Fig. 24
Daca in fata modelului aflat in
polariscop se plaseaza pe directia σ2, o platbanda din acelasi material si de aceeasi grosime, se poate reduce intirzierea intre cele doua componente ale
luminii care traverseaza modelul, prin tensionarea epruvetei cu σl- σ Intirzierea este redusa la zero (compensare
totala), atunci cind imaginea epruvetei privita prin analizor se intuneca (fig.
4 ). Pentru o determinare mai exacta a ordinului de acest tip de compensator este
recomandat sa fie folosit in lumina alba.

Fig. 25
In fig. 26
se prezinta schematic un compensator cu epruveta de tractiune. Epruveta E, este
montata intr-un inel rigid I. Incarcarea
se realizeaza printr-un dispozitiv
cu filet micrometric S, etalonat in prealabil. Intreg sistemul se poate roti pe un cadran gradat C, putind fi blocat intr-o pozitie
oarecare cu ajutorul surubului de blocare B.
Pentru determinarea ordinului de banda
intr-un punct se procedeaza astfel:
se determina parametrul izoclinei in punctul
respectiv utilizind lumina alba
polarizata plan;
-se
asaza modelul in
polariscopul cu lumina polarizata circular,utilizind sursa de lumina alba;
-se
fixeaza compensatorul cu epruveta orientata in lungul uneia din directiile tensiunilor principale determinate in punctul considerat din model;
-se
incarca compensatorul pina cind se observa, pe epruveta o banda intunecata marginita de doua benzi galbene
intr-o parte si cealalta.Ordinul de
banda in epruveta este acelasi cu cel din model. In
cazul in care nu se obtine banda intunecata
insemneaza ca compensatorul a fost orientat pe directia σ si este
necesar sa se roteasca cu 90°.
Notand cu
P sarcina cu care a fost incarcat compensatorul ,cu n
si h dimensiunile transversal ale epruvetei si tinand seama ca in cazul
epruvetei σ se poate scrie:
 (52)
(52)
Din (45) si (46),avand in
vedere ca σ2=0 rezulta k=σ1h/σ'o (53)
Unde σ'o=constanta fotoelastica a
materialului.
Aceasta metoda de compensare pe langa
faptul ca permite determinarea valorilor fractionare ale ordinului de banda
dintr-un punct al modelului,mai da posibilitatea identificarii tensiunilor
σ si
5.COMPENSAREA CU COMPENSATORUL BABINET-SOLEIL
Metoda de compensare Babinet-Soleil
consta in introducerea pe langa model,in campul polariscopului cu lumina
polarizata circular,a unei alte surse de birefrigerenta.In fig.27 se prezinta
suprapunerea efectelor optice produse d ecele doua surse de
birefrigerenta.Compensatorul Babinet-Soleil consta din doua lame de cuart L1 si
L2,una de grosime constanta t1,iar cealalta de grosime variabila t2,fiind
alcatuita din doua parti in forma de pana.Efectul optic produs de cele doua
pene de cuart este aditiv si proportional cu grosimea totala.Una dintre penele
de cuart este fixa,iar cealalta se poate deplasa in lung prin rotirea unui
surub micrometric esalonat S,realizandu-se astfel variatia grosimii t2 a
lamei.Cuartul este un material care prezinta birefrigerenta permanenta.
Cele doua
lame de cuart L si L2 sint montate cu axele optice perpendicu-
 Fig. 27
Fig. 27
lare,
astfel ca in mod normal cind lama L2 are grosimea maxima t , se
obtine extinctia totala.Intirzierea
totala produsa de compensator cind este introdus in polariscop poate fi variata
continuu prin modificarea grosimii lamei t2 cu ajutorul surubului micrometric t Cind t1
= t2 intarzierea impusa
este
zero, iar cind compensatorul mareste
sau micsoreaza intirzierea rezultanta. In acest caz se recomanda sa se foloseasca
lumina monocromatica.
Pentru
determinarea ordinului de banda fractionar cu acest instrument se procedeaza astfel:
-se determina directiile
tensiunilor principale in punctul considerat din model;
-se plaseaza
compensatorul in polariscop in fata modelului in dreptul punctului considerat, cu axa optica paralela cu
directia tensiunii ;
-se roteste surubul micrometric pina cind se
obtine extinctie totala in punctul respectiv. Citirile
facute pe scala surubului micrometric sint proportionale cu ordinul de banda din
punctul cercetat.
Sa presupunem
ca punctul in care urmeaza sa fie determinat ordinul de banda (notat cu A in fig. 28) se afla intre izocromatele de
ordinul 3 si 4, iar constanta aparatului este k = 1,8 diviziuni/ordin de banda. Plasind instrumentul in A, sa presupunem ca extinctia totala se
obtine prin rotirea surubului
micrometric pina la diviziunea 6,5. Tinind seama ca ordinul de banda k = 3 corespunde la 3 x
1,8 = 5,4 diviziuni, ordinul de banda in punctul A va fi kA
In felul acesta ordinul de banda in punctul A poate fi determinat cu o precizie de trei
zecimale.Metoda de compensatie Tardy
este cea mai folosita in practica pentru determinarea ordinului de banda intr-un punct din model, deoarece nu necesita echipament sau instrumente auxiliare. In acest caz se folosese elementele
optice ale polariscopului circular. Sa
presupunem ca elementele polariscopuhii sint aranjate pentru cimp intunecat si
ca in jurul punctului A, in care
urmeaza sa se determine ordinul de banda, se observa franjele din fig. 28.
De asemenea, se considera ca directiile tensiunilor principale din punctul A aU
fost determinate anterior si sint cunoscute. Pentru determinarea ordinului de banda in punctul A, se
procedeaza astfel :
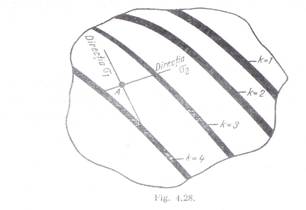
6.COMPENSAREA PRIN METODA TARDY
-se roteste intreg
sistemul optic al polariscopului (polarizor, analizor si ambele lame sfert de unda), mentinindu-se
aceeasi pozitie relativa intre ele, pina cind axele polarizorului si
analizorului se aliniaza cu axele tensininilor
principale din punctul A (in acest caz franjele observate nu se modifica) ;
se roteste analizorul cu n grade pina cind
se obtine extinctie totala, astfel ca banda de ordinul 3 sa se deplaseze
spre punctul A. Ordinul de banda in
acest caz se modifica cu n/180 din valoarea intreaga, astfel ca ordinul de
banda corespunzator punctului A va fi,
kA=3+(n/180)
Aceasta valoare poate fi verificata daca rotim analizorul in sens invers
cu m grade, pina cind se obtine extinctia totala, astfel
ca franja de ordinul 4 sa se deplaseze spre
punctul A. In acest caz,kA=4-
Pentru verificare trebuie
ca 3+
Dupa cum se observa aceasta
metoda este foarte simpla si rapida permitind determinarea cu precizie a ordinului de
banda in orice punct al modelului. Precizia acestei metode depinde de
calitatea lamelor sfert deunda cu care este echipat polariscopul.
7. MULTİPLİCAREA ORDİNULUİ DE BANDĀ
Metodele de compensare folosite pentru
determinarea valorilor frac-tionare
ale ordinului de banda care au fost prezentate mai sus, prezinta doua neajunsuri : 1) necesita determinarea prealabila a
directiilor tensiunilor principale in
punctele de interes, 2) furnizeaza informatii in puncte discrete, reducind astfel fotoelasticitatea la o
metoda de analiza punct cu punct.
Utilizind un sistem de semioglinzi, D.
Post a stabilit o tehnica noua de
compensare care permite determinarea simultana cu precizie, a valorilor fractionare ale ordinului de banda in
toate punctele modelului. In acest
scop polariscopul standard cu lumina polarizata circular a fost modificat asa cum rezulta din fig. 29.
Polariscopul este
prevazut cu doua lentile de cimp L1 si L2 care fac ca modelul sa fie traversat de un fascicul de
raze paralele si totodata, au rolul
de a focaliza intr-un plan razele transmise prin semioglinda.
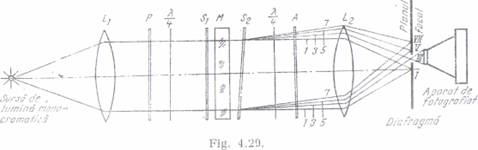
Modelul fotoelastic este
asezat intre doua semioglinzi Sl si S2 dintre caire
una (S ) este perpendiculara pe axa
polariscopului iar cealalta (S2) este usor inclinata. Efectul optic produs de
semioglinda inclinata S asupra
luminii care traverseaza modelul in cele doua sensuri este
prezentat in fig. 30. Dupa cum se observa,
fieoare raza de lumina iese din semioglinda S2 sub un anumit unghi care
depinde de numarul de traversari ale modelului. Astfel, raza 1 traversind modelul o singura data se
transmite prin
semioglinda S2 sub unghiul 0°, raza 3 traverseaza modelul de trei ori si se transmite prin
semioglinda sub unghiul 2φ, raza 5 traverseaza modelul de cinci ori si se transmite sub unghiul 4 , s..a.rn.d. Deoarece diferitele raze de lumina care ies din semioglinda S2
sint inclinate sub diferite unghiuri fata de
axa polariscopului, este posibil ca fiecare raza sa fie izolata.In
acest sens razele sunt focalizate in diferite puncte situate in planul focal al lentilei L Pentru a izola imaginile celorlalte puncte, de regula, se f oloseste o diafragma care permite vizualizarea imaginii
corespunzatoare unui anumit factor de multiplicare. Astfel in fig, 29 aparatul
defotografiat este
aranjat sa fotografieze o imagine a
modelului in care franjele
izocromate sint multiplicate de 3 ori (n=3).In figura 31 se prezinta imaginea unui model la care franjele
izocromate au fost multiplicate de
trei respectiv de cinci ori.
Fig. 30.
Franjele izocromate corespunzatoare date de razele 1, 3, 5,
etc.
pot fi fotografiate atit in cimp luminat cit si in cimp intunecat. Se considera, de exemplu ca se
fac fotografii in cele doua cimpuri pentru razele 1, 3 si 5. Franjele inregistrate prin fotografierea imaginii I in cele doua
cimpuri vor reprezenta valorile
ordinului de banda in succesiunea : k =0 ;1/2;1;3/2;2;5/2 etc.cele
corespunzatoare imaginii III vor da k=0;1/6;1/3;1/2;2/3;5/6 etc,iar cele
obtinute pentru imaginea V vor da k=0;1/10;1/5;3/10;2/5;1/2 etc.Suprapunind
datele inregistrate din aceste determinari se poate determina valoarea
ordinului de banda cu mare precizie
in toate punctele modelului.
Dupa cum se vede in fig. 30 lungimea
drumului pe care il strabate lumina in modelul fotoelastic depinde de unghiul
de inclinare φ al semioglinzii S2,
de numarul de traversari ale modelului, cit si de distanta dintre oglinzi. Toti acesti factori fac ca in cazul
unor multiplicari de sapte rezultatele
obtinute prin utilizarea acestei metode sint de asemenea determinate de calitatea semioglinzilor depinzind
foarte mult de coeĢicientii de
reflexie R si de transmisie T ai acestora. Astfel, pentru obtinerea unui factor de
multiplicare egal cu cinci, care este suficient pentru majoritatea aplicatiilor, se recomanda folosirea unui
set de semioglinzi avind coeficientul
de reflexie R = 0,67, respectiv de transmisie T
= 0,33, in care una din
semioglinzi sa fie inclinata.cu un unghi
Prin utilizarea semioglinzilor in
polariscopul cu lumina polarizata circular se mai pot obtine si alte
efecte optice deosebit de importante pentru
cercetarile de fotoelasticitate, cum este efectul de ,,ascutire
a franjelor'. Astfel daca cele doua semioglinzi sint paralele intre
ele, datorita reflexiilor multiple ale
razelor care strabat modelul, se obtine o subtiere pronuntata a franjelor albe si negre care apar
simultan pe un fond gri. In felul acesta utilizind efectul ,,ascutirii franjelor' se pot obtine pe aceeasi fotografie franje intunecate care
corespund la valorile 0 ; 1; 2 ; 3, etc. ale ordinului de banda si
franje luminate care corespnnd la valorile ordinului de banda ―;3/2;5/2 etc.
5. SEPARAREA TENSİUNİLOR
PRİNCİPALE FOLOSİND DETERMİNĀRİLE
FOTOELASTİCE
Dupa cum s-a
aratat in paragrafele precedente, prin metoda fotoelastica se pot determina directiile
principale, cu ajutorul izoclinelor si diferenta tensiunilor principale σ - σ2, cu ajutorul izocromatelor.
Pentru

cunoasterea
starii de tensiuni in orice punct al modelului trebuie determinate valorile individuate si σ2 ale tensiunilor principale. Cu exceptia contururilor neincarcate,
in lungul carora se pot determina tensiunile principale
direct din determinarile fotoolastice, separarea tensiunilor principale
se face fie utilizind ecuatiile diferentiale de echilibru pentru starea plana
de tensiuni, fie folosind alte metode auxiliare prin care se determina suma tensiunilor principale , asa cum se va vedea in paragraful
6.
5.1.
DETERMINAREA TENSIUNILOR PE UN CONTUR
NEINCĀRCAT
Se stie ca, in general, tensiunile
maxime apar pe conturul pieselor si de aceea, din punct de vedere
practic, pentru dimensionarea corecta a pieselor,
este importanta cunoasterea acestor tensiuni. Curba de variatie a tensiunilor
pe conturul neincarcat al unei piese se poate trasa cu usurinta cu ajutorul izocromatelor obtinute prin
fotoelasticitate.
Daca se considera, un element de volum marginit de conturul neincarcat al unei piese, supusa la o stare plana de tensiune
(fig. 32, a), atit tensiunea normala σy
cit si cea tangentiala π sint
nule. Prin urmare, conturul in acest caz este o
fata principala. Cercul lui Mohr fiind tangent in origine la axa π
(fig. 32, b), rezulta ca diferenta tensiunilor principale (σ - σ2)c pe acest contur, este egala cu tensiunea
principala orientata dupa directia tangentei la contur. Daca un punct i
de pe contur este intersectat de izocromata de
ordinul k (fig. 33), tensiunea
in acest punct are valoarea
(σ1i)c=k σ (55)
unde σ este constanta
fotoelastica a modelului.
Reprezentind la scara valorile (σ1)c calculate in punctele de intersectie ale izocromatelor cu conturul, se obtine diagrama
de variatie a. tensiunilor pe conturul
neincarcat (fig. 33).
Semnul tensiunilor pe contur se
poate deduce, in general, din modul de
solicitare a piesei. Cind acest lucru nu e posibil, se poate folosi metoda ,,probei cu virf ascutit'. Pentru
aceasta se apasa conturul cu virful unei
surubelnite, de exemplu.
si se urmareste evolutia izocromatelor.
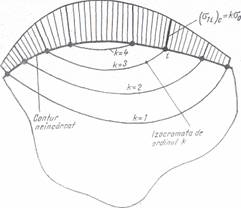 Figura 33
Figura 33
Presupunind ca tensiunea principala σ
orientata dupa tangenta la contur este
pozitiva, starea de tensiuni poate fi reprezentata prin cercul trasat cu o linie continua in fig. 34, a. Tensiunea
normala la contur σ produsa de virf, fiind de compresiune va avea ca
efect marirea diametrului cercului, trasat
cu linie intrerupta in aceeasi figura, ceea ce inseamna marirea ordinului izocromatei pe contur. In cazul ca
ordinul izocromatelor este crescator spre
contur, ca in fig. 34, b, se observa ca izocromata de pe contur este deplasata spre interior, in locul ei
aparind izocromata de ordin superior.
Daca
tensiunea principala σ2 paralela cu tangenta la contur este de compresiune, deci negativa, starea de tensiuni pe
contur este reprezentata prin cercul
trasat cu linie continua in fig. 34, c. Aplicarea pe contur a unei sarcini de compresiune face ca diametrul
cercului sa se micsoreze si sa scada ordinul izocromatei. Daca se
considera, ca si in cazul precedent, ca
ordinul izocromatelor create spre contur, in punctul in care se aplica sarcina de compresiune, izocromatele din interior
se vor deplasa catre contur, ca in fig 3 d.
Aceasta metoda de
stabilire a semnului tensiunilor pe contur poate fi folosita mai ales
atunci clnd izocromatele au un traseu aproximativ
paralel cu conturul si ordinul izocromatei
pe contur corespunde unei tensiuni mai
mari decit cea care se naste prin apasarea virfului.
Fig. 3
5. METODA DIFERENTEI TENSIUNILOR TANGENTIALE
Metoda diferentei tensiunilor
tangentiale, elaborata de Frocht, permite
determinarea tensiunilor principale pe o directie oarecare din model,
pornind de la un punct in care aceste tensiuni sint cunoscute, de exemplu de pe un contur neincarcat.
Integrind prima din
ecuatiile (56) se
obtine 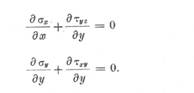
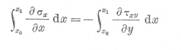
sau, exprimind pe (58) prin diferente finite (fig. 36),
rezulta :
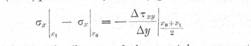
unde σx|x1
si σx|x sint tensiunile normale in punctele x1
respectiv x0 de pe directia
aleasa, Δx,Δy sint intervalele
finite pe directiile x respectiv y.
Deci, tensiunea normala intr-un punct x1
se poate calcula cunoscind tensiunea in punctul x0 precum
si variatia tensiunii tangentiale πxy
pe
directia y, in
mijlocul intervalului {la
Daca punctul initial x0
se ia pe contur, tensiunea principala paralela cu tangenta la contur se poate determina cu
relatia (55) cunoscind ordinul izocromatei pe contur.In cazul ca directia aleasa x, este normala la
contur, σ2|x0= x|x0 0.
Daca axa y face un unghi α0 cu tangenta la contur, iar tensiunea principala paralela cu tangenta este σ1|xo,tensiunea
σx|Xo se calculeaza cu relatia:
σx|Xo σ1|xo sinēαo (60)
Tensiunile
tangentiale pe directiile AB respectiv CB se pot determina cunoscind izocromatele si izoclinele care
intersecteaza aceste directii, cu relatia:
 (61)
(61)
Diferenta tensiunilor
principale in punctul considerat k, se
deduce din ordinul izocromatei
cu relatia
σ1 - σ2 =k σo (62)
unghiul α fiind parametrul izoclinei in acelasi
punct.
Trecand la punctul x se poate scrie relatia:
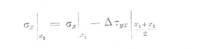 (63)
(63)
Cu care se determina σx|X2 procedand analog ca pentru σx|X1 Procedeul se repeta pentru
celelalte puncte de pe directia x. Pentru verificare este
bine ca punctul final sa se gaseasca
tot pe un contur neincarcat in care tensiunile
sint cunoscute.
Tensiunile σy se
calculeaza cu relatia:
σy= σx
-( σ1 - σ2)cos 2α= σx-k σo cos
2α (64)
unde, asa cum s-a aratat mai sus, k este ordinul izocromatei, αa
este constanta fotoelastica a modelului, iar α este
parametrul izoclinei.Pentru determinarea tensiunilor principale se porneste
de la observatia ca, intr-un punct, suma
tensiunilor principale este constanta
σx
+ σy= σ1+ σ2 (65)
Pe de alta parte, diferenta tensiunilor principale rezulta din
relatia
Rezolvind
sistemul format din ecuatiile (62) si (65) se obtine valorile individuale ale tensiunilor
principale:
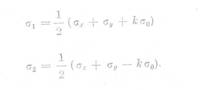 (66)
(66)
Pentru sistematizarea calculelor se poate.
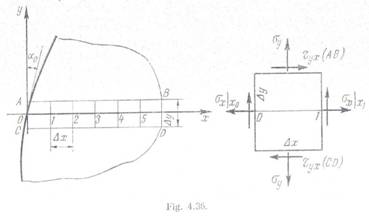
proceda astfel (fig. 37, a). Se traseaza pe o foaie de
calc izoclinele si izocromatele pentru domeniul in care urmeaza sa se determina tensiunile principale. Se traseaza dreapta in lungul careia se vor calcula tensiunile
principale si se divizeaza intr-un numar
de segmente egale Δx.De asemenea se mai duc liniile AB si D,paralele uc directa aleasa,la distanta Δx=
Δy In general, prin
nodurile retelei astfel obtinute nu trec nici izocline si nici
izocromate stfel ca determinarea directiilor principale si a
ordinului izocromatelor in noduri se face
prin interpolare. Pentru aceasta, se traseaza curbele de 'variatie a unghiului
directiilor principale in lungul segmentelor AB si respectiv CD, (fig.
37, b), precum si curbele de variatie a ordinului izocromatelor (fig.. 37, c). Unghiurile α (parametrii
izoclinelor) precum. si ordinul k al izocromatelor in punctele 1', 2',
3', si 1', 2', 3', de pe
direcfiiile AB respectiv CD, se trec de regula intr-un tabel
(tabelul 2). Cu aceste
valori se calculeaza tensiunile tangentiale in aceleasi puncte.
Tensiunile σx si σy din
tabelul 2 au fost determinate mai intai in
functie de ordinul izocromatei (coloanele 7, 12 si 14), iar apoi prin multiplicare
cu σ0 = 15 daN/cm2·franje au fost calculate in daN/cm2
(coloanele 13, 15, 16). In final, in
coloanele 17 si 18 sint date tensiunile principale σ si
calculate cu relatiile (66).
Precizia
rezultatelor obtinute prin metoda descrisa depinde de precizia cu care sint inregistrate izoclinele si izocromatele
deoarece erorile se cumuleaza.
Deoarece in calcule nu sint necesare decit izoclinele si izocromatele care, in general, se pot inregistra cu
suficienta exactitate, metoda este relativ simpla iar precizia este
comparabila cu cea data de alte metode, astfel ca majoritatea autorilor o
recomanda pentru separarea tensiunilor principale.
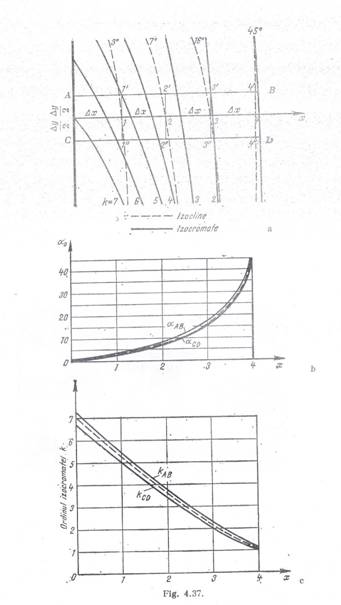 FIGURA 37
FIGURA 37
Sistematizarea calculelor pentru
determinarea valorilor individuale ale tensiunilor principale
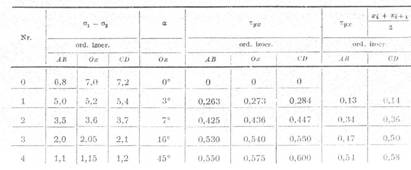 Tabel
2
Tabel
2
5.3. METODA APROXİMATİVĀ ,,RAPID'
Metoda ,,Rapid', elaborata tot de Frocht , poate fi utilizata
pentru separarea tensiunilor principale in sectiunile de simetrie in cazul
barelor de sectiune dreptunghiulara cu
crestaturi, sau cu gauri simetrice, solicitate la intindere sau la
compresiune axiala precum si la incovoiere pura. Aceste seetiuni corespund unei directii principale.
Folosind izocromatele
(fig. 38) se traseaza curba de variatie a dife-

Fig. 38
rentei tensiunilor principale in
sectiunea de simetrie (fig. 39). Din. Identitatea
σ1= (σ1
- σ2 σ2 (67)
rezulta relatia dintre ordonatele curbelor,
care reprezinta variatia tensiu-nilor σ1 , σ respectiv σ1 - σ Derivind relatia (67) rezulta si
relatia intre pantele
tangentelor la aceste curbe:
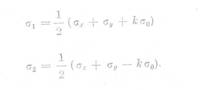 (68)
(68)
folosind determinarile foloelestice(ordinul de
banda k si parametrul izoclinelor α) Tab.
sau, folosind notatiile din fig. 39.
tg
a = tg β- tgγ (69)
Tinand seama si de conditiile po contur, se obtin
elemente suficiente pentru trasarea aproximativa a curbelor σ1 si σ2,
care se corecteaza apoi verificand indeplinirea simultana a conditiilor
date de relatiile (67), (68). Asa cum s-a
aratat, pe un contur neincarcat se pot separa tensiunile principale, una din tensiuni (cea
normala la contur) fiind nula. In aceste puncte se
poate determina si unghiul y dintre
axa de simetrie si tangenta la curba de
variatie a tensiunii principale normala la contur.
Constructia
este usurata, daca se cunosc in plus puncte in care tensiunea σ2 are valori extreme. Conform teoremei lui Mesnager
o
tensiune principala are un maxim in punctele in care izostatica si izoclina corespnnzatoare se intersecteaza in unghi drept.
In fig 39 s-au trasat curbele σ si σ pentru
cazul din fig. 38 al unei bare de sectiune dreptunghiulara cu crestaturi
laterale in ,,V" rotunjite la baza cu o raza
de racordare ρ, solicitata la incovoiere pura.
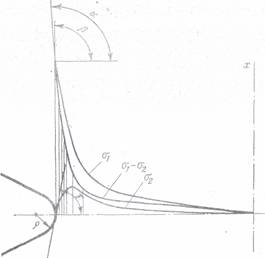
Fig. 39.
5.METODA DE INTEGRARE DE-A LUNGUL UNEİ İZOSTATİCE
Metoda Consta in integrarea ecuaciilor
L'ame-Maxwell in lungul unei izostatice . Spre
deosebire de metodele descrise in paragrafele precedente,
la care era suficienta cunoasterea izoclinelor si a izocromatelor, la aceasta metoda trebuie sa
se traseze izostaticele cu metoda descrisa in paragraful
Considerind o izostatica S1 (fig.
40) care porneste dintr-un punct 0, situat pe contur, precum si
izostaticele de speta a doua care o intersecteaza in punctele 1,2,3, prin integrarea primei ecuacii Lame-Maxwell se obtine:
 (70)
(70)
Sau,cu diferente finite:
 (71)
(71)
Daca se cunoaste tensiunea
intr-un punct S10 si valoarea medie a
Raportului [(σ1 -
σ2)/ρ2] pe intervalul Δs1; ,se
poate calcula tensiunea σ 1|s in punctul S de pe izostatica S (fig. 40).

Fig. 40.
Rationamentul se repeta
pentru punctele urmatoare. Daca punctul initial se ia pe un contur neincarcat, valoarea σ1 |sl1
se determina direct daca se cunoaste ordinul
izocromatei in acel punct cu relatia cunoscuta (55). De asemenea, diferenta tensiunilor principale se
determina tot din tabloul izocromatelor cu
relatia (62).
In cazul ca prin punctul
considerat nu trece nici o izocromata, ordintul k, al izocromatei se
poate determina prin interpolare, trasind curba de variable a ordinului izocromatelor in lungul
izostaticei alese. Mai dificila este determinarea cu
precizie a razelor de curbura p2 ale izostaticelor de speta a doua.
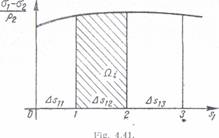
Pentru efectuarea calculelor se poate
folosi metoda tabelara, ca la metoda diferentei tensiunilor tangentiale,
sau se reprezinta diagrama de variatie a valorilor si se
planimetreaza aria marginita, Ω fig. 41), care reprezinta
valoarea integralei din membrul al doilea al relatiei
Tensiunea intr-un punct i,
σ1 |Sli va fi data de relatia:
σ |Sli = 1|S10 - (72)
5.5. METODA DE NTEGRARE DE-A LUNGUL UNE ZOSTAT CE FOLOSİND UNGHİUL DİNTRE
İZOCLİNE Sİ
İZOSTATİCE
Ecuatiile
Lame-Maxwell pot fi puse si sub o alta forma, cea data
de Filon. Daca se considera elementul limitat de doua perechi de izostatice si se scriu elementele de arc sub forma ds1
= ρ dα1, ds2 = ρ 2dα2
ecuatiile (57) devin
 (73)
(73)
Fie α
parametrul izoclinei care trece prin originea sistemului (fig, 42) si α + Δα
parametrul izoclinei care trece prin punctul A. Unghiurile dintre
tangentele la izostatice vor fi egale cu Δα. Daca se noteaza cu Ψ
unghinl dintre tangentele in 0 la
izostatica S si la izoclina si cu Ψ' unghiul
dintre tangenta in B la
izostatica S2 si izoclina (fig. 42) pentru Δs1 = ds1 si
Δs2 = ds2
se poate considera ca unghiul OAB = 180° - Ψ, iar unghiul - 90˚ si deci
(Δs1/Δs2)=ctg (180˚ - Ψ)=- ctg Ψ (74)
De asemenea, din figura 42 mai
rezulta si relatia:
 Relatia 74
Relatia 74
Termenul (σ1 - σ2) ctg ΨΔα reprezinta
valoarea medie a produsului pentru punctele S10 si S11.
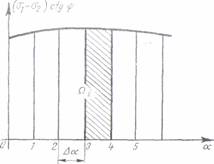 Figura 44
Figura 44
Pentru a
aplica aceasta metoda, se traseaza in lungul izostaticei izoclinele consecutive, al caror parametru
difera cu .
In punctele de intersectie
se determina ordinul izocromatei si unghiul dintre izostatica si
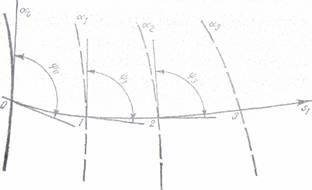 Figura. 43
Figura. 43
izoclina (fig. 43). Daca punctul 0 se afla pe contur,
σ1|S se poate calcula cunoscind ordinul izocromatei si constanta
fotoelastica a modelului cu relatia (55).
Datele pot fi trecute intr-un tabel, asemanator cu cel
utilizat la metoda diferentei tensiunilor
tangentiale, sau se poate trasa curba de variable a valorilor (σ1 - σ2) ctg Ψ
in functie de parametrul izoclinelor. Aria Ωi marginita de aceasta curba, (fig. 44),permite calculul tensiunilor principale intr-un punct oarecare i cu relatia
σ1| s1i =σ |S i
Metoda da rezultate bune in cazul cind
unghiurile Ψ au
valori apropiate de 90°. In cazurile in care unghiurile sint mici, deci
izoclinele sint aproape paralele cu
izostatica, erorile la determinarea valorilor ctg
sint mari. In aceste cazuri se recomancla folosirea metodei
descrisa in paragraful urmator.
5.6. A DOUA METODA DE INTEGRARE IN LUGUL
UNEI
IZOSTATICE
Metoda a fost elaborata tot de Filon
si se poate aplica in cazul sectiunilor de simetrie, care sint si
izostatice si in lungul caror a unghiurile dintre izocline si izostatice sint mici. Ecuatiile
Lame-Maxwell se pun sub urmatoarea forma,
tinind seama de relatiile dintre elementele de arc, razele de curbura si
parametrul izoclinei
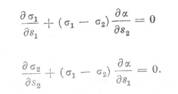 Rel. 76
Rel. 76
Integrand prima dintre aceste ecuatii se obtine:
 Rel.77
Rel.77
Ca si in cazurile
precedente se porneste de pe un contur neincarcat, in care se cunoaste valoarea tensiunii principale,
iar intervalele Δs1 se pot lua egale. In punetele 0,1, 2, se determina ordinul izocromatelor si lungimea
arcului de izostatica s2 limitat de doua izocline succesive. Pentru o precizie satisfacatoare parametrul izoclinelor
trebuie sa varieze cu mai putin de 5' (Δα
= 5°). Aplicind metoda tabelara se pot calcula succesiv tensiunile principale in punctele 0, 1,2, De asemenea, se poate reprezenta curba de
variatie a valorilor
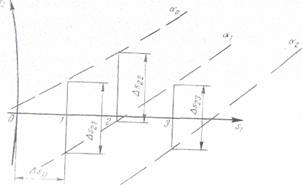 Figura 45
Figura 45
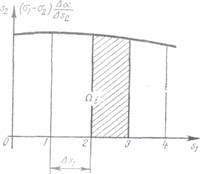 Figura 46
Figura 46
(σ1 -
Δα / Δs2) in
lungul izostaticei si
sa se planimetreze aria marginita, Qi (fig. 46).
5.7. METODA İNCİDENTEİ
OBLİCE
Dupa cum
s-a aratat, atunci cind un model fotoelastic plan este traversal prin incident a normala de un
fascicul de lumina
polarizata,legatura dintre diferenta tensiunilor principale si
ordinul de banda intr-un puuct P, este data de relatia (45).
Tinind seama de (45) si (46) se poate scrie:
Fig. 47.
= k(σo'/h) (78)
sau
notand A1=(
rezulta A1 - A2=k (80)
Considerind tensiunea principala σ3
= 0, se roteste modelul fotoelastic cu unghiul Φ in jurul directiei
tensiunii principale σ1 (fig. 47).Lungimea
drumului parcurs de lumina prin model in acest caz va fi h/cosΦ, iar tensiunile principale din planul
principal pe directia de propagare a
luminii sint σ1si σ
cos2 Φ. Inlocuind aceste valori in expresia (78) si
notind cu k ordinul de banda, determinat
in acelasi punct P, prin incidenta oblica , se obtine:
Sau tinand seama de (79) se mai
poate scrie 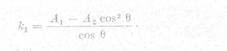
Din (80) si (81) se obtine:
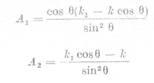
Sau tinand seama de (46) se
obtine
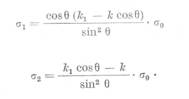 (83)
(83)
In felul acesta.
cu ajutorul expresiilor (83) pot fi determinate valorile individuale ale tensiunilor
σ1 si σ2 intr-un punct P, atunci cind se cunosc valorile ordinelor de banda inregistrate in acest
punct prin cele doua moduri de incidenta (normala si oblica) si unghiul
cu care se roteste modelul.Daca modelul se roteste in jurul directiei
tensiunii principale σ2,
notind cu k2 ordinul de
banda citit in acest caz in punctul P, valorile individuale ale
tensiunilor principale vor fi date de urmatoarele expresii care se deduc asemanator.
 (84)
(84)
Dupa cum s-a. mai putut observa
pentru determinarea valorilor individuale ale tensiunilor principale intr-un
punct din model, este necesar sa se cunoasca in prealabil directiile acestor
tensiuni in punctul considerat. Pentru a obtine o diferenta cit mai mare intre
ordinele de banda (k si
k1) citite prin cele doua moduri de incidenta,
se recomanda sa se lucreze cu unghiuri de incidenta
ale luminii cit mai mari. Uneori marimea unghiulul de incidenta este limitata de neclaritatea franjelor, care apar estompate
in zonele in care gradientul tensiunilor este ridicat. Alegerea acestui unghi
se face in functie de geometria modelului si modul de incarcare, astfel ca franjele observate prin incidenta oblica sa apara cit mai clare. In aplicarea acestei metode
trebuie sa se tina seama de fenomenul de refractie care apare la intrarea si iesirea luminii
din model. Neglijarea fenomenului de refractie poate uneori sa
conduca la erori importante in determinarea valorilor individuale ale
tensiunilor. De aceea pentru eliminarea acestui efect, mai ales in cazul in care se lucreaza cu unghiuri mari de incidenta, se recomanda introducerea modelului
fototoelastic intr-o cuva cu pereti transparenti in care se afla un lichid cu
indicele de refractie egal cu cel al materialului fotoelastic. Cuva trebuie sa aiba peretii plani, iar lumina polarizata sa intre in
cuva prin incidenta normala.
In practica
experimentala, pentru determinarea tensiunilor principale prin incidenta oblica, uneori se mai folosesc
polariscoape construite special , care utilizind metoda lui Favre, masoara
intirzierea dintre cele doua componente ale
luminii care traverseaza modelul prin incidenta oblica. Acest tip de
polariscop prezinta dezavantajul ca reduce analiza
fotoelastica obisnuita la o analiza punct cu
punct.




 Detaliul A
Detaliul A














 Figura 33
Figura 33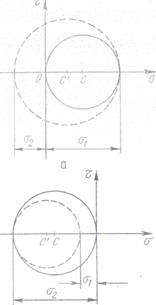


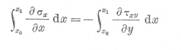

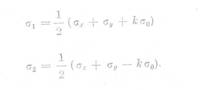 (66)
(66)




 (70)
(70) (71)
(71)

 (73)
(73)
 Figura 44
Figura 44 Figura. 43
Figura. 43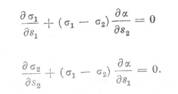
 Figura 45
Figura 45 Figura 46
Figura 46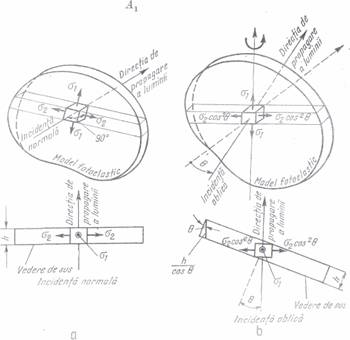
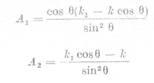
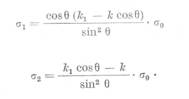 (83)
(83) (84)
(84)