Prelucrarea marimilor masurate direct

Prelucrarea marimilor masurate direct

1 Marimi masurate direct si de aceeasi precizie

Considera ca asupra unei marimi au fost efectuate observatiile in acealeasi conditii de mediu, cu acelasi instrument si de catre acelasi observator (observatii de aceeasi precizie). Valoarea probabila a marimii masurate notata cu se obtine cu relatia:

Eroarea mediei aritmetice (a valorii probabile) obtinuta cu relatia se noteaza cu si se obtine cu relatia:

in care:

- eroarea medie patratica a unei singure masuratori;

- numarul de masuratori.

Daca sunt erorile aparente date de egalitatiile:

reprezinta  eroarea medie, care se calculeaza ca fiind o eroare medie patratica a erorilor reale.

Respectiv

Sau:

In expresia minim (pincipiul micilor patrate, iar din expresiile

Din relatia rezulta:

-eroarea medie patratica a mediei aritmetice este direct proportionala cu eroarea medie patratice a unei singure masuratori;

-eroarea medie patratica este invers proportionala cu numarul de masuratori.Ca urmare, poate fi realizat graficul unei iperbole ( din care:

Rezulta

-eroarea scade sensibilitatea cu cresterea numarului

de masuratori ();

-eroarea creste cu scaderea numarului de   

masuratori .

Exemplu:

Observatiile efectuate asupra unei lungimi au valorile:

; ; ; ; ;

Toleranta admisa este =1cm. 

Analizand in prima etapa valorile observatiilor se constata:

- are valoare mult diferita fata de celelalte

- conduce la un ecart maxim de 1,1 cm

Ca urmare:

-se elimina , asupra acesteia a actionat o eroare inadmisibila;

- se elimina , pentru ca se impune <.

Se calculeaza

O prima constatare: toleranta a fost considerata, pentru ca:

x

Se calculeaza

Rezultatul final se scrie:

2 Functii de marimi masurate direct si cu aceeasi precizie

De cele mai multe ori, in practica apare o anumita categorie de masuratori, la care o marime sau mai multe marimi nu pot fi accesibile la masuratori directe, ci trebuie deduse din masuratori efectuate asupra altor marimi masurate direct si cu aceeasi precizie.

Marimile care trebuie determinate sunt legate de marimile masurate prin functii care pot fi explicite si implicite.

Astfel

a) Suma unghiurilor intr-un triunghi nu poate fi masurata direct, ci numai unghiurile individual

b) Diferenta de nivel intre doua puncte determinate prin nivelment trigonometric c;

c) Coordonatele unui punct determinate prin metoda intersectiei inainte;

Dezvoltand exemplul a) avem:

Functia este explicita si liniara, de la care putem generaliza:

Sau matriceal:

in care: ;

Pentru exemplu b) avem:

Functia este explicita, dar neliniara, sau generalizand:

Pentru exemplul c) consideram coordonatele punctelor cunoscute si unghiurile masurate

Se va stabili:

ω>0   

cu care valorile compensate ale unghiurilor sunt:

=

=

=

Unghiurile care exprima orientarile directiilor si sunt:

coordonatele ale punctului lui se obtin din ecuatiile:

-= 0

-= 0

Se observa ca relatiile , avand in vedere reprezinta doua functii neliniare si implicite care pot fi scrise altfel:

Forma generala a unor astfel de functii este:

   

. . . . . . . . . . . . . . .

Functii neliniare explicite sau implicite pot fi liniarizate pentru a determina erorile unor astfel de functii pe baza erorilor marimilor masurate.

In acest scop, consideram functia in care sunt afectate de erori de masurare ce pot fi asimilate cu cresterile . Functia va avea cresterea si in consecinta putem scrie:

Prin dezvoltare in serie Taylor se obtine:

=++ 

Notam : ;

si atunci:

In situatia in care o functie neliniara, implicita sau explicita este liniarizata, ne aflam in situatia functiilor liniare si ca urmare se disting:

a) functii liniare;

b) functii explicite;

c) functii neliniare implicite.

Pentru acestea erorile pot fi:

a) ;

b) ;

c) functiile liniare implicite reprezinta cazul general al functiilor de marime masurate direct.

Aceste functii exista atunci cand:

Pentru a determina erorile functiilor exista doua posibilitati:

Prima posibilitate consta in rezolvarea sistemului . Se obtine:

. . . . . . . .

Si in continuare se aplica relatia

Este un procedeu greoi si nu se aplica.

A doua posibilitate consta in liniarizarea in prealabil a functiilor . Se obtine in acest fel un sistem de ecuatii in cresterile care se rezolva in raport cu

In cele din urma se aplica relatia

Pentru simplificare introducem notatiile:

Se observa ca se obtine din prin inlocuirea coloanelor coeficientilor cresterilor cu terminii liberi.

Prin raportul dintre cu rezulta coeficintii cresterilor pe care-i notam cu si avem:

=

Sau:

=

in care:

si:

3 Marimi masurate direct de precizii diferite

Consideram ca asupra unui unghi orizontal au fost efectuate observatii in aceleasi conditii, dar in serii diferite, in care numarul de observatii a fost

Deci:

Valoarea probabila a marimii masurate M se obtine cu relatia:

in care:

o - media observatiilor din serii;

p - ponderea observatiilor din serii stabilite cu egalitatea:

eroarea mediei aritmetice ponderate se obtine cu egalitatea:

in care:

- eroarea medie patratica a unitatii de pondere

Functii de marimi masurate direct de precizii diferite

Forma functiilor ca si in cazul masuratorilor directe de aceeasi precizie poate fi: liniara, neliniara explicita si neliniara implicita.

Erorile acestor functii se obtin cu relatiile similare: , dar in care intervin ponderilor marimilor din functie.

Astfel:

- pentru functii liniare:

- pentru functii neliniare explicite:

- pentru functii neliniare implicite:

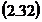
in care:

;  ;