Dinamica miscarii oscilatorii

Dinamica miscarii oscilatorii

In continuare sunt prezentate cele mai importante cazuri de oscilatii simple cu un singur grad de libertate. Asupra unui oscilator pot sa actioneze mai multe tipuri de forte: forte elastice F_e forte de frecare F_f sau forte perturbatoare F_p. In functie de numarul si tipul fortelor care actioneaza asupra corpului care oscileaza se disting mai multe tipuri de oscilatori:

Oscilator liber, neamortizat: F_e 0, F_p = 0 si F_f = 0.

Oscilator liber, amortizat: F_e 0, F_p = 0 si F_f

Oscilator neamortizat si intretinut: F_e 0, F_p 0 si F_f = 0.

Oscilator amortizat si intretinut: F_e 0, F_p 0 si F_f

Oscilatorul liber neamortizat

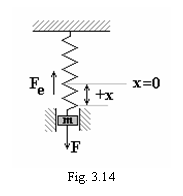Cel mai simplu caz este acela al unui oscilator liber neamortizat. Modelul mecanic corespunzator acestui oscilator este prezentat in figura 3.14. Acesta modeleaza comportarea unui sistem mecanic, suspendat cu un element elastic de masa neglijabila, de un reper fix. Se actioneaza asupra sistemului cu o forta F, deplasandu-l fata de pozitia de echilibru cu alungirea x. In elementul elastic va apare o forta elastica F_e, care este proportionala cu alungirea x, in cazul unor deplasari mici fata de pozitia de echilibru. Atunci cand sistemul este lasat liber, forta elastica va cauta sa aduca, tot timpul, sistemul in pozitia initiala de echilibru. Sistemul va efectua o miscare de oscilatie liniara. Daca se ingradeste miscarea, astfel incat sa se execute numai dupa o singura directie (verticala, de exemplu), oscilatia va avea un singur grad de libertate. Se neglijeaza frecarile sistemului cu aerul sau cu alt mediu, precum si pierderile de energie in sistemul elastic.

Forta elastica va imprima sistemului o acceleratie pe care o vom nota cu . Ea simbolizeaza derivata a doua a elongatiei in raport cu timpul. Legea a doua a mecanicii aplicata acestui sistem mecanic oscilant se poate scrie:

(1)

Aceasta este o ecuatie diferentiala omogena de ordinul 2 care mai poate fi scrisa si sub forma:

(2)

sau in urma impartirii cu m si tinand cont de relatia (3.1.10), sub forma:

(3)

Una din modalitatile de rezolvare a acestei ecuatii diferentiale omogene consta in scrierea ecuatiei caracteristice a acesteia si apoi in rezolvarea ecuatiei caracteristice. Pentru ecuatia diferentiala data de relatia (3), ecuatia caracteristica este:

(4)

avand radacinile imaginare:

(5)

Solutia ecuatiei diferentiale va fi o combinatie liniara a celor doua radacini ale ecuatiei caracteristice, de forma:

(6)

sau daca se scrie cu ajutorul functiilor armonice, in cazul radacinilor imaginare, de forma:

(7)

Deci, miscarea sistemului mecanic este o oscilatie armonica de amplitudine A, pulsatie w si faza initiala j

Amplitudinea si faza initiala a oscilatiei depind de conditiile initiale ale sistemului si pot fi determinate daca se cunosc acestea.

In cazul general, conditiile initiale sunt:

la t = 0 (8)

Aceste conditii conduc la urmaturul rezultat:

la t = 0 (9)

Inlocuind cele doua constante C₁ si C₂ in relatia (7) se obtine ecuatia de miscare a oscilatorului liber neamortizat:

(10)

Se poate observa ca, in functie de conditiile initiale, ecuatia miscarii poate sa fie sinusoidala sau cosinusoidala. Astfel, daca la t = 0, x = si = 0, ecuatia miscarii este o functie cosinus, ca in figura 3.2, de forma: (11)

Daca la t = 0, x = 0 si ecuatia miscarii este o functie sinus, ca in figura 3.2, de forma:

(12)

Oscilatorul liber amortizat cu forta de frecare vascoasa

Oscilatiile libere neamortizate sunt idealizari deoarece, in natura si tehnica, toate oscilatiile sunt mai mult sau ami putin amortizate. Amortizarea se poate datora atat frecarii "uscate" a sistemului care oscileaza cu un alt corp rigid (de exemplu, frecarea axului unui piston in lagar sau cu peretii cilindrului) cat si frecarii "vascoase" a sistemului cu fluidul in care oscileaza (aerul sau un alt fluid vascos).

In continuare este prezentat doar cazul amortizarii oscilatiilor datorita frecarilor corpului care oscileaza cu un mediu fluid si vascos.

Modelul mecanic al unui astfel de oscilator, care oscileaza cu frecare fata de un mediu vascos, este prezentat in figura 3.15.

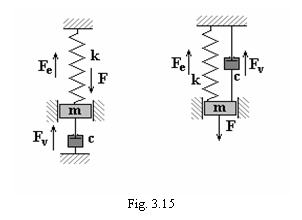Ecuatia de miscare a acestui sistem se obtine scriind legea a doua a dinamicii, conform careia corpul de masa m se misca accelerat, cu acceleratia sub actiunea rezultantei celor doua forte: forta elastica si a fortei de frecare vascoasa :

(13)

Forta de frecare vascoasa este proportionala cu viteza de deplasare a sistemului in mediul vascos, constanta de proportionalitate c fiind coeficientul de amortizare vascoasa, specific fluidului in care are loc oscilatia.

Trecand toti termenii in membrul stang se obtine ecuatia diferentiala a miscarii oscilatorii, care este o ecuatie diferentiala omogena de ordinul doi:

(14)

Impartind aceasta relatie cu m se obtine:

(15)

sau:   (16)

in care s-au folosit notatiile: patratul pulsatiei proprii de oscilatie a sistemului;

factorul de amortizare vascoasa.

Scriind ecuatia caracteristica corespunzatoare ecuatiei diferentiale omogene de ordin doi se obtine: (17)

Prin rezolvarea ecuatiei caracteristice se obtin solutiile:

(18)

In functie de semnul cantitatii de sub radical se intalnesc trei situatii:

, radacinile sunt imaginare, complex conjugate;

, radacinile sunt reale si egale;

, radacinile sunt reale si distincte.

In cazul radacinilor reale si egale si coeficientul de amortizare este:

(19)

Aceasta valoare a coeficientului de amortizare se numeste coeficient critic de amortizare notat c_cr.

Pentru un anumit sistem oscilant, coeficientul critic de amortizare depinde numai de masa sistemului si de constanta elastica a elementului elastic.

Cele trei cazuri prezentate anterior:

, sau c < c_cr , miscarea este periodica, subcritica (cazul frecarilor mici);

, sau c = c_cr ,miscarea este aperiodica, critica;

, sau c > c_cr ,miscarea este aperiodica, supracritica (cazul frecarilor mari).

In continuare se vor analiza cele trei cazuri.

miscarea subcritica

Cantitatea se noteaza cu si radacinile ecuatiei caracteristice sunt:

(20)

Solutia ecuatiei diferentiale se poate scrie :

(21)

Solutia poate fi scrisa si cu ajutorul functiilor armonice sinus si cosinus, aplicand relatiile de transformare ale lui Euler, din functii exponentiale in functii armonice:

(22)

sau:   (23)

Aceasta ecuatie a fost stabilita pentru prima data in 1980 de catre Borda (1773-1799), studiind miscarea oscilatorie a unui pendul.

Cele doua constante A si j pot fi exprimate in functie de cele doua constante C₁ si C₂ conform relatiilor (3.3.6) si (3.3.7). Constantele C₁ si C₂ se determina la randul lor din conditiile initiale, care in cazul general sunt:

la t = 0 (24)

Aplicand aceste conditii initiale se obtine:

la t = 0 (25)

deci:  (26)

Inlocuid cele doua constante C₁ si C₂ in expresia amplitudinii A si a fazei initiale j se obtine:  (27)

si:  (28)

Solutia ecuatiei diferentiale (sau ecuatia de miscare a oscilatorului) va avea expresia:

(29)

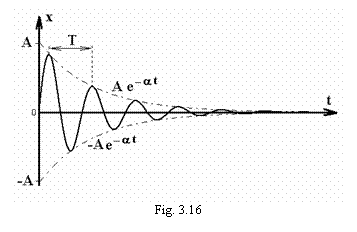
Deci, oscilatia rezultanta va avea pulsatia b, iar amplitudinea scade exponential in timp. O astfel de oscilatie amortizata poate fi reprezentata grafic ca in figura 3.16.

In ecuatia de miscare a oscilatorului marimea b care joaca rolul unei pulsatii se numeste pseudopulsatie si are expresia:

(30)

Cu cat oscilatia este mai puternic amortizata, cu atat pseudopulsatia b este mai mica decat pulsatia proprie de oscilatie a sistemului neamortizat.

Marimea: (31)

Se numeste pseudoperioada si este totdeauna mai mare decat perioada proprie de oscilatie a sistemului neamortizat

O masura a gradului de amortizare a oscilatiilor in regim subcritic o reprezinta decrementul logaritmic d, ce caracterizeaza scaderea in timp a amplitudinii oscilatiei amortizate. Decrementul logaritmic este definit ca fiind logaritmul natural al raportului dintre elongatia miscarii x(t) la un anumit moment de timp si elongatia miscarii x(t + T) dupa scurgerea unui interval de timp egal cu o pseudoperioada. Raportul elongatiilor este:

(32)

iar decrementul logaritmic d este:

(33)

O alta marime ce caracterizeaza scaderea in timp a amplitudinii oscilatiei este constanta de timp t sau timpul scurs din momentul initial pana cand amplitudinea oscilatiei scade de e ori. Constanta de timp este:  t =     (34)

deoarece amplitudinea oscilatiei dupa timpul t este:

miscarea critica

In cazul in care radacinile ecuatiei caracteristice sunt reale si egale sau c = c_cr.

Solutia ecuatiei diferentiale este de forma:

(35)

Cele doua constante C₁ si C₂ pot fi determinate si in acest caz din conditiile initiale, care in cazul general sunt:   la t = 0 (36)

Rezolvand acest sistem, se obtine ecuatia de miscare:

(37)

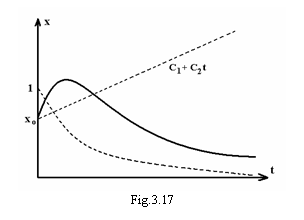Graficul miscarii sistemului, in cazul amortizarii critice, este prezentat in figura 3.17 pentru cazul in care x₀ > 0 si v₀ > 0. Miscarea sistemului este aperiodica, iar dupa un anumit interval de timp sistemul revine in pozitia de echilibru (x = 0).

miscarea supracritica

Atunci cand , sau c > c_cr, radacinile ecuatiei caracteristice sunt reale si distincte. Ecuatia de miscare a sistemului este o combinatie liniara a doua functii exponentiale, in care apar la exponent cele doua radacini ale ecuatiei caracteristice r₁ si r₂.

(38)

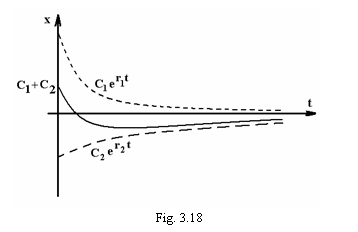
Miscarea sistemului este de asemenea aperiodica, iar graficul miscarii amortizate, aperiodice, supracritice este prezentat in figura 3.18, pentru cazul in care C₁ > 0 si C₂ < 0.

Cele doua constante C₁ si C₂ pot fi determinate si in acest caz din conditiile initiale, ecuatia de miscare a sistemului fiind de forma:

(39)