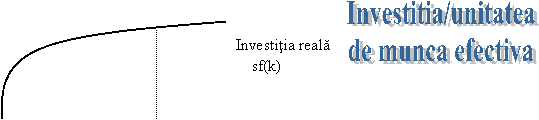Starea stabila in modelul solow de crestere economic

Starea stabila in modelul solow de crestere economic

MODELUL LUI SOLOW

Reprezinta punctul de plecare pentru aproape toate analizele privind cresterea economica. In plus alte abordari sunt mai usor de inteles daca se face referire la acest model.

Ipoteze:

1. Ipoteze privind functia de productie:

Functia de productie are randamente de scara constante, i.e. c > o , avem: F(cK, cAL) = cF(K,AL), caci:

economia este suficient de mare pentru ca posibilitatile de specializare sa fie aproape epuizate; economii mici pot exista posibilitati

alte intrari in afara de munca, capital si cunoastere sunt neimportante. (resursele naturale nu-s o problema pentru tarile dezvoltate).

Forma intensiva a functiei de productie, f(k), satisface urmatoarele proprietati (Inada):

f(0) = 0; f'(k) > 0; f''(k) < 0; f'(0) = ; f'(

2. Evolutia stocurilor de capital, munca si cunostinte

L'(t) = nL(t); A'(t) = gA(t) (3)

Partea din venitul agregat (output) destinata investitiei este considerata exogena si constanta, s, iar rata uzurii capitalului este d. Astfel:

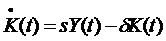(4)

Singura restrictie este ca parametrii, n+g+d > 0

Dinamicile modelului:

Prin transformari succesive a ecuatiei (4) se obtine o forma intensiva pentru dinamica lui k: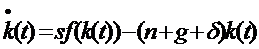

- ecuatia principala a modelului lui Solow.

Ecuatia arata ca rata de modificare a stocului de capital/unitatea de munca efectiva este egala cu diferenta dintre: s*f(k) - investitia reala/unitatea de munca efectiva si

(n+g+d)k(t) - investitia punctului critic, i.e. volumul investitiei care trebuie facuta doar pentru a pastra pe k la nivelul existent.

Chiar daca investitia asigura pastrarea constanta a stocului de capital K, aceasta nu-i suficient pentru pastrarea lui k constant.

Cand investitia/unitatea de munca efectiva depaseste investitia pragul critic al k creste, de nu k scade (vezi figura nr.1).

Fie k* solutia ecuatiei k'(t) = 0, corespunzatoare maximului lui k. Se poate observa ca exista o relatie intre k'(t) si k(t). Realizand o translatie convenabila se poate obtine urmatoarea diagrama de faza pentru k (fig. 2)

(n+g+d)k

k'

k*  k

Fig. 1. Investitia reala si de prag critic.   

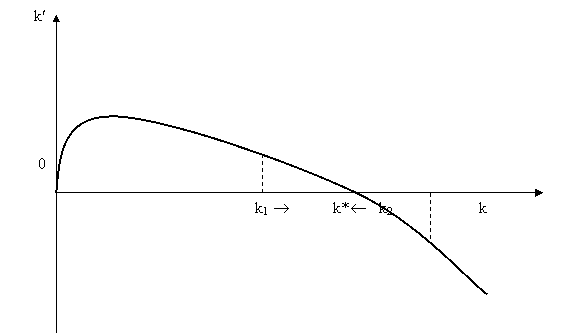
Fig. 2. Diagrama de faza a modelului Solow

Daca, initial k₁ < k*, => investitia reala depaseste investitia de prag critic, => k' > 0, i.e. k creste.

Daca, k₂ > k* => k < 0.

Pt k = k* => k' = 0     (k nivel maxim).

Calea de crestere echilibrata

Din moment ce k tinde (converge) spre k* => intrebarea:

cum se comporta variabilele modelului pentru k = k*.

Prin definitie munca si cunoasterea cresc in ratele n si g (vezi ecuatiile de start). Stocul de capital K = Alk*; din moment ce k este constant (=k*), K va creste cu rata n+g (i.e. K'/K = n+g). Daca atat capitalul cat si munca efectiva cresc cu rata n+g, din conditia de randamente de scara constante => ca si Y creste cu aceiasi rata.

In final, capitalul/lucrator (inzestrarea tehnica a muncii), K/L, si productia pe lucrator, Y/L, cresc cu rata g.

Astfel, modelul lui Solow implica faptul ca indiferent de punctul de start, economia converge spre o cale de crestere echilibrata - o situatia unde fiecare variabila a modelului creste cu o rata constanta.

Pe o astfel de cale de crestere, rata de crestere a output/lucrator este determinata numai de rata progresului tehnic - g

In cele mai multe tari dezvoltate, se poate aproxima oarecum, ca ratele de crestere ale capitalului, muncii si productiei au fost oarecum constante.