Determinarea solutiilor optime in cazul functiilor
criteriu  si
si 
Determinarea solutiilor optime in cazul
utilizarii functiilor criteriu  si
si  poate fi
ilustrata prin considerarea unor sisteme de reglare automata de ordinal II,
avand in stare inchisa functii de transfer
poate fi
ilustrata prin considerarea unor sisteme de reglare automata de ordinal II,
avand in stare inchisa functii de transfer  cu
polinoame de gradul II la numitor.
cu
polinoame de gradul II la numitor.
a.
Aplicarea criteriului  in cazul
unei functii de transfer cu doi poli.
in cazul
unei functii de transfer cu doi poli.
Considerand un sistem de ordinul II cu
functia de transfer (2.50), folosirea relatiei (2.11) conduce la expresia
 (3.21)
(3.21)
si identificand
coeficientii din (2.18) si (3.21) rezulta



 (3.22)
(3.22)


 Fiind satisfacuta conditia (2.19), se
utilizeaza relatiile (2.25), (2.26), (2.27), (2.28) si (2.29) rezultand
Fiind satisfacuta conditia (2.19), se
utilizeaza relatiile (2.25), (2.26), (2.27), (2.28) si (2.29) rezultand


 (3.23)
(3.23)




Inlocuind (3.23) si (3.24) in (2.25)
se obtine
 (3.25)
(3.25)
Pentru determinarea valorii optime  se
anuleaza derivate
se
anuleaza derivate
 (3.26)
(3.26)
rezultand
 (3.27)
(3.27)
(avand in vedere
conditia  , pentru asigurarea stabilitatii sistemului [1]).
, pentru asigurarea stabilitatii sistemului [1]).
Din (3.25) se
constata ca nu exista o valoare finita  care sa
minimizeze criteriul
care sa
minimizeze criteriul  , valoarea criteriului fiind cu atat mai mica, cu
cat valoarea
, valoarea criteriului fiind cu atat mai mica, cu
cat valoarea  este mai mare; acelasi
rezultat se obtine si din expresia
derivatei criteriului
este mai mare; acelasi
rezultat se obtine si din expresia
derivatei criteriului  din - (3.25) - in
raport cu
din - (3.25) - in
raport cu  :
:
 (3.28)
(3.28)
care se anuleaza
numai daca
 (3.29)
(3.29)
Aceasta concluzie este intru totul
justificata, avand in vedere faptul ca la sistemele de reglare automata cu
functia de transfer (2.50) suprareglajul depinde numai de valoare  , iar modificarea valorii
, iar modificarea valorii  determina numai o
contractare sau dilatare (in directia axei timpului) a raspunsului y al
sistemului la un semnal treapta
determina numai o
contractare sau dilatare (in directia axei timpului) a raspunsului y al
sistemului la un semnal treapta  [1].
Astfel, in figura 3.1 este reprezentat raspunsul
[1].
Astfel, in figura 3.1 este reprezentat raspunsul  al unui system cu
al unui system cu  si
si  , iar in figura 3.2 - raspunsul
, iar in figura 3.2 - raspunsul  al unui
system cu
al unui
system cu  si
si  , constatandu-se ca in al doilea caz
, constatandu-se ca in al doilea caz
sunt evident mai
mici ariile delimitate de raspunsul y in raport cu orizontala valorii
stationare  , deci si criteriul
, deci si criteriul  va avea in
al doilea caz o valoare mai mica decat in primul caz; deoarece
va avea in
al doilea caz o valoare mai mica decat in primul caz; deoarece  , suprareglajul este egal la cele doua raspunsuri.
, suprareglajul este egal la cele doua raspunsuri.
Intrucat in cazul considerat optimizarea
valorii  nu poate fi
obtinuta numai prin intermediul criteriului
nu poate fi
obtinuta numai prin intermediul criteriului  , este necesara introducerea unui criteriu
suplimentar. In practica, acesta poate fi reprezentat de respectarea largimii
de banda impuse
, este necesara introducerea unui criteriu
suplimentar. In practica, acesta poate fi reprezentat de respectarea largimii
de banda impuse  , care
asigura proprietatiile de filtru ale sistemului si deci o comportare dorita in
raport cu perturbarile de inalta frecventa [1], conform unei conditii de forma
, care
asigura proprietatiile de filtru ale sistemului si deci o comportare dorita in
raport cu perturbarile de inalta frecventa [1], conform unei conditii de forma
 (3.30)
(3.30)
unde  este
largimea de banda a sistemului.
este
largimea de banda a sistemului.
Ca urmare, pentru valoarea  din (3.27) se
considera relatia corespunzatoare dintre largimea de banda
din (3.27) se
considera relatia corespunzatoare dintre largimea de banda  si
pulsatia
si
pulsatia  , care are
aspectul [1]
, care are
aspectul [1]
 (3.31)
(3.31)
si se adopta pentru  valoarea limita admisa de conditia (3.30) , deci
valoarea limita admisa de conditia (3.30) , deci
 (3.32)
(3.32)
Din (3.31) si (3.32)
se obtine

deci rezulta
valoarea  considerata
ca optima
considerata
ca optima
 (3.33)
(3.33)
In privinta valorii  din (3.27) se
constata ca regimul tranzitoriu va avea un suprareglaj relative ridicat,
intrucat pentru sistemele cu functia de transfer (2.50) valorii
din (3.27) se
constata ca regimul tranzitoriu va avea un suprareglaj relative ridicat,
intrucat pentru sistemele cu functia de transfer (2.50) valorii  ii
corespunde [1] suprareglajul
ii
corespunde [1] suprareglajul
 (3.34)
(3.34)
Acest rezultat confirma faptul (mentionat
in paragraful 5.2.1) ca criteriul  conduce la
valori mai mari ale suprareglajului in comparatie cu criteriul
conduce la
valori mai mari ale suprareglajului in comparatie cu criteriul  , acestuia din urma corespunzandu-i procesul
tranzitoriu etalon aperiodic (3.6) ,
datorita faptului ca are loc si limitarea valorilor derivatei
, acestuia din urma corespunzandu-i procesul
tranzitoriu etalon aperiodic (3.6) ,
datorita faptului ca are loc si limitarea valorilor derivatei 
b. Aplicarea criteriului  in cazul
unei functii de transfer cu doi poli si un zero.
in cazul
unei functii de transfer cu doi poli si un zero.
Considerand ca functia de transfer a
sistemului inchis poate fi pusa sub forma
 (3.35)
(3.35)
urmeaza sa fie determinata valoarea optima  a
parametrului a prin intermediul
criteriului
a
parametrului a prin intermediul
criteriului 
Identificand (3.35) cu forma obisnuita a
functiilor de transfer cu doi poli si un zero [1]
 (3.36)
(3.36)
rezulta
 (3.37)
(3.37)
 (3.38)
(3.38)
 (3.39)
(3.39)
deci prin
determinarea valorii  se obtin
valorile optime pentru
se obtin
valorile optime pentru  si z.
si z.
Inlocuind (3.35) in (2.11) se obtine
 (3.40)
(3.40)
si identificand
coeficientii din (2.18) si (3.40) rezulta



 (3.41)
(3.41)


Intrucat este
satisfacuta conditia (2.19), se folosesc relatiile (2.25), (2.26), (2.27), (2.28)
si (2.29) rezultand









 (3.43)
(3.43)

Inlocuind (3.42) si (3.43) in (2.25) se obtine
 (3.44)
(3.44)
anularea
derivatei
 (3.45)
(3.45)
conducand la
valoarea optima
 (3.46)
(3.46)
(din (3.38) si (3.39)
rezultand conditia a > 0).
Inlocuind (3.46) in (3.38) si (3.39)
rezulta
 (3.47)
(3.47)
 (3.48)
(3.48)
Intrucat valorile  si
si  sunt
functii de parametrii regulatorului, din (3.47) si (3.48) rezulta implicit
valorile de acordare optima a acestor parametrii.
sunt
functii de parametrii regulatorului, din (3.47) si (3.48) rezulta implicit
valorile de acordare optima a acestor parametrii.
Astfel, de exemplu, presupunand ca partea fixata are o functie de transfer
 (3.49)
(3.49)
si se alege o
structura de regulatoare PI, cu functia de transfer aproximativa [1]
 (3.50)
(3.50)
rezulta

si
 (3.51)
(3.51)
Identificand
coeficientii numaratorilor din (3.35) si (3.51) se obtine



si inlocuind (3.46) in (3.52)
rezulta



Punerea functiei
de transfer sub forma (3.35) permite optimizarea in functiei de un singur parametru, a,
ceea ce simplifica considerabil obtinerea solutiei optime.
In subcapitolul 5.4 este ilustrata cautarea
optimului unei functii criteriu dependete de mai multi parametri.
c. Aplicarea criteriului  in cazul
unei functii de transfer cu doi poli.
in cazul
unei functii de transfer cu doi poli.
Considerand functiile de transfer (2.48)
si (2.50), criteriul  are
expresia (2.93), obtinuta in paragraful 5.1.4 prin intermediul functiilor
Liapunov; expresia criteriului
are
expresia (2.93), obtinuta in paragraful 5.1.4 prin intermediul functiilor
Liapunov; expresia criteriului  poate fi
obtinuta usor si prin intermediul trelatiilor directe din paragraful 5.1.3.
poate fi
obtinuta usor si prin intermediul trelatiilor directe din paragraful 5.1.3.
Pentru ilustrare, se considera
expresia  din (3.21) -
obtinuta pentru functia de transfer (2.50) - si se aplica relatiile (2.33) si (2.35) rezultand
din (3.21) -
obtinuta pentru functia de transfer (2.50) - si se aplica relatiile (2.33) si (2.35) rezultand
 (3.54)
(3.54)
prin
identificarea coeficientilor din (2.37) si (3.54) se obtine





verificandu-se conditia (2.38).
Prin intermediul
relatiilor (2.40) se obtin expresiile



deci pentru (2.39)
rezulta forma
 (3.57)
(3.57)
Determinand  se obtine conform relatiilor (2.28) si (2.29)
se obtine conform relatiilor (2.28) si (2.29)
 (3.58)
(3.58)
- avand in vedere
(3.55) - iar determinantul Δ este cel din (3.24) .
Ca urmare,
inlocuind in (3.57) expresiile (3.55), (3.56), (3.58) si (3.24) se
obtine
 (3.59)
(3.59)
Introducand in (2.32) expresiile (3.25) si (3.59)
rezulta
 (3.60)
(3.60)
Pe de alta parte, inlocuind (2.51), (2.52)
si (2.53) in (2.93) se obtine
 (3.61)
(3.61)
identitatea
expresiilor (3.60) si (3.61) confirmand faptul ca prin relatii directe si prin
intermediul functiilor functiilor Liapunov se obtine acelasi rezultat pentru
functia criteriu 
Anuland derivatele expresiei  in raport cu
in raport cu  si cu
si cu  , din (3.61) rezulta
, din (3.61) rezulta
 (3.62)
(3.62)

Pentru o valoare  , din (3.42) se obtine
, din (3.42) se obtine
 (3.63)
(3.63)
iar pentru o valoare  , din (3.63) rezulta
, din (3.63) rezulta
 (3.64)
(3.64)
Din (3.63) si (3.64)
se constata ca adoptand o valoare initiala pentru  (sau pentru
(sau pentru  ), determinand valoarea corespunzatoare
), determinand valoarea corespunzatoare
 (respectiv
(respectiv  ) si reactualizand apoi
succesiv valorile
) si reactualizand apoi
succesiv valorile  si
si  se obtine un proces care nu converge spre o
pereche de valori optime ale celor doi parametri, intrucat valorile acestora
cresc continuu cu fiecare pas de cautare a optimului.
se obtine un proces care nu converge spre o
pereche de valori optime ale celor doi parametri, intrucat valorile acestora
cresc continuu cu fiecare pas de cautare a optimului.
Acest rezultat
se datoreste faptului - mentionat anterior in legatura cu expresia (3.29) si
ilustrat prin figurile .5.1 si 5.2 - ca in cazul sistemelor cu functia de
transfer (2.50) cresterea valorii  determina o reducerea a ariilor delimitate de
raspunsul y in rapot cu valoarea stationara
determina o reducerea a ariilor delimitate de
raspunsul y in rapot cu valoarea stationara  .
.
De aceea este
indicat ca valoarea  sa fie aleasa din considerentul satisfacerii
conditiei (3.30) , impuse pentru largimea
de banda, iar valoarea
sa fie aleasa din considerentul satisfacerii
conditiei (3.30) , impuse pentru largimea
de banda, iar valoarea  sa fie obtinuta din (3.63) prin introducerea
valorii
sa fie obtinuta din (3.63) prin introducerea
valorii  respective; intrucat valoarea
respective; intrucat valoarea  nu este inca cunoscuta - cum a fost in cazul (3.27) - si
deci nu poate fi direct stabilita o dependenta de tipul (3.31) intre
nu este inca cunoscuta - cum a fost in cazul (3.27) - si
deci nu poate fi direct stabilita o dependenta de tipul (3.31) intre  si
si  (deoarece aspectul dependentei este in functie
de valoarea
(deoarece aspectul dependentei este in functie
de valoarea  ), pot fi necesare cateva
iteratii, incepand cu o dependenta adoptata initial intre
), pot fi necesare cateva
iteratii, incepand cu o dependenta adoptata initial intre  si
si  , determinand valoarea
, determinand valoarea  - printr-o relatie de tipul (3.33) -
inlocuind-o in (3.63) si reactualizand dependenta mentionata in conformitate cu
valoarea
- printr-o relatie de tipul (3.33) -
inlocuind-o in (3.63) si reactualizand dependenta mentionata in conformitate cu
valoarea  gasita etc.
gasita etc.
In orice caz, din (3.63) se verifica faptul -
mentionat in paragraful 5.1.1 - ca criteriul  conduce la
o calitate mai buna a regimului tranzitoriu, in comparatie cu criteriul
conduce la
o calitate mai buna a regimului tranzitoriu, in comparatie cu criteriul  , deoarece pentru orice valoare
, deoarece pentru orice valoare  (obtinuta
in functie de
(obtinuta
in functie de  ) din (3.63) va rezulta o valoare
) din (3.63) va rezulta o valoare  mai mare
decat cea din (3.27) , obtinuta prin
criteriul
mai mare
decat cea din (3.27) , obtinuta prin
criteriul  pentru aceeasi functie
de transfer (2.50), ceea ce corespunde unui suprareglaj
pentru aceeasi functie
de transfer (2.50), ceea ce corespunde unui suprareglaj  mai mic
[1].
mai mic
[1].
d. Aplicarea criteriului  in cazul
unei functii de transfer cu doi poli si un zero.
in cazul
unei functii de transfer cu doi poli si un zero.
Considerand ca partea fixata are o functie de trasnfer de forma

(valorile parametrilor  si
si  fiind cunoscute) si ca se adopta un bloc de
reglare PI, cu functia de trasnfer
fiind cunoscute) si ca se adopta un bloc de
reglare PI, cu functia de trasnfer

se obtin expresiile functiilor de
transfer ale sistemului deschis si inchis


si ale transformatelor  si
si 
 (3.65)
(3.65)

 (3.66)
(3.66)
conform cu (2.11)
si (2.36), in ipoteza unei variatii treapta unitara a marimii de referinta.
Aplicand relatiile (2.25) . (2.29)
pentru expresiile (3.65) si (3.66) se obtin componentele  si
si  ale criteriului
ale criteriului 


rezultand

conform cu (2.32).
Pentru obtinerea
valorilor optime  ,
,  ale parametrilor regulatorului se calculeaza
derivatele partiale
ale parametrilor regulatorului se calculeaza
derivatele partiale

si

Din anularea
primei derivate partiale
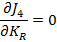
se obtine

iar din anularea celeilalte
derivate partiale

rezulta

Introducand in
expresiile functiilor de transfer H(s) si  valorile optime
valorile optime  si
si  rezulta
rezulta

si

Din expresia H(s)
se constata ca raspunsul la o variatie treapta a marimii de referenta are
aspectul unei exponentiale cu constanta
de timp T, deci se obtine chiar procesul tranzitoriu etalon din (3.6) . Inlocuind
valorile optime  si
si  in expresia criteriului
in expresia criteriului  rezulta
rezulta


confirmandu-se
astfel obtinerea valorii  din (3.7) , intrucat
din (3.7) , intrucat  pentru raspunsul la treapta unitara.
pentru raspunsul la treapta unitara.



 (3.51)
(3.51)






