Utilizare de programe utilitare specializate pe diferite domenii

Ce este un program utilitar specializat ?

In diferitele domenii de specialitate (medicina, matematica, fizica, chimie, inginerie, design, etc.) au fost dezvoltate de-a lungul ultimului deceniu o mare varietate de programe (software) care ruleaza pe computere din ce in ce mai performante si care acopera o paleta larga de utilizari in domeniul respectiv, incepand cu partea dedicata invatarii (Learn to speak English, Matematica, etc.) pana la cele mai sofisticate simulari sau prelucrari de date (Statistica, SPSS, Matlab, Maple etc.).

Nu exista domeniu actual care sa nu aiba acoperita cu programe de calculator toate partile sale importante. Indiferent insa de domeniu, toate aceste programe au o ,filosofie' comuna privind modul de lucru si interfata cu utilizatorul. Diferentele specifice apar atunci cand este vorba de introducerea si prelucrarea datelor prin tehnici specifice.

& Tipuri de interfete de initializare

Cand rulam un astfel de program, prima ,luare de contact' se refera la ,fereastra' de initializare, care ne pune in contact direct cu tipurile de optiuni furnizate de program.

Dam mai jos patru astfel de exemple pentru patru programe diferite.

1. Programul Statistica

Un program des utilizat in aplicatiile statistice profesioniste este cel furnizat de firma Statsoft.inc si denumit generic Statistica. Atunci cand pornim acest program, prima fereastra, cea de initializare, arata astfel.

Din fereastra de meniuri de mai sus se alege meniul care ne intereseaza, de exemplu "Basic Statistic/Tables" ales cu ajutorul comenzii Switch To, dupa care obtinem fereastra de lucru standard de mai jos.

  

Se observa ca aceasta fereastra reprezinta o fereastra activa, de lucru, pe care, stiind caracteristicile datelor si legile de lucru, o putem folosi pentru a lansa diferite aplicatii. Se observa asemanarea ei cu o fereastra ,clasica' tip Windows.

2. Programul SPSS

Programul SPSS care este tot un program specializat foarte cunoscut de statistica are fereasta de initializare sub forma.

dupa care se ,intra' in fereastra normala de lucru.

Se observa usor faptul ca la cele doua programe, ferestrele de lucru sunt asemanatoare.

3. Programul MAPLE

Programul Maple este un program utilitar general de matematica, folosit in foarte multe universitati de renume din intreaga lume, fereastra sa de initializare aratand ca mai jos.

Odata initializat, fereastra de lucru a acestui programe arata astfel.

4. Programul STELLA

Programul Stella este un program de simulare in sisteme dinamice aplicate in biologie, fizica, chimie, etc. si care, plecand de la date concrete prelevate din natura simuleaza fenomenul care sta la baza acestora. Fereastra sa de lucru arata ca mai jos.

Utilizare programului MS PowerPoint

& Programul Microsoft PowerPoint

Programul MS PowerPoint este cel mai cunoscut program de computer folosit pentru prezentari digitale de orice fel. El face parte din grupul de programe MS Office, alaturi de MS Word si MS Excel.

Poate fi folosit cu succes in prezentari stiintifice, prezentari publicitare, prezentari de firme, prezentari statistice, etc. Se bazeaza mult pe inter-conectivitatea cu MS Word si MS Windows, putand-se copia documente sau parti de documente intre ele. Adaugand functii multimedia audio/video si animatie, prezentarea in PowerPoint devine deja o arta.

Lucru in PowerPoint

Pentru a deschide programul se face dublu clic pe icon-ul respectiv sau se cauta programul in Start / Programs /PowerPoint asa cum se vede in figura de mai jos.

Dupa deschiderea programului, va aparea fereastra de lucru urmatoare, din care alegem tipul de slide si fundalul corespunzator folosind secventa Format / Apply design template

Dupa apasarea butonului Apply se ajunge la fereastra de lucru sub forma slide-ului care poate fi completat cu text sau formule si tabele.

Dupa completarea unui slide se trece la un nou slide prin secventa Insert / New slide.

Un slide normal arata ca in figura de mai jos, putand completa textul atat pe slide cat si spatiul de lucru din stanga, depinzand de setarea particulara a programului.

Odata ce toate slide-urile au fost completate putem trece la prezentarea ,filmului' format din secventa de slide-uri respective prin secventa Slide show / View show, asa cum se observa mai jos.

Utilizarea programului MAPLE

Sintaxa: modul in care sunt puse in ordine, cuvintele, expresiile, operatorii pentru a forma o propozitie coerenta.

Sintaxa programului Maple (exemple):

a , b  a sequence of values

a -> b an operator (simple procedure)

a or b logical or

a and b    logical and

not a  logical not

a < b  comparison operations

a <= b

a = b  

a <> b

a > b

a >= b

a .. b a range of values

a mod b    an expression or value mod another value

a + b - c   arithmetic operations

+ a  

- a

a union b  set union and difference

a minus b  

a * b / c   arithmetic operations

a intersect b  set intersection

a &* b inert and matrix multiplication

a ^ b   exponentiation

a !    factorial

( a )  a parenthesized expression (to control precedence)

' a '  unevaluated expression

< a >  mapped to a call to anglebracket

a set

[ a, b, ]  a list

f ( a )    function call

Aplicatii practice

1. Functii

Grafice de functii. Se utilizeaza sintaxa plot.

> plot(f(x), x=ab, y=cd, options);

x = ab se refera la axa absciselor

y = cd se refera la axa ordonatelor; consideram ca este deseori necesara utilizarea acestui ultim argument.

options se refera la eventualele optiuni legate de reprezentarea grafica

Exemple:

Desenati graficele functiilor utilizand Maple

si

> plot(sqrt(x^2+1),x = -77,y = 07, linestyle=1, labels=[x,y],

xtickmarks = 6, ytickmarks = 6);

> plot((ln(x))*(x^(- 1)),x=07,y=-71,linestyle=4,labels=[x,y],

xtickmarks=6, ytickmarks=6);

Pentru a desena o functie definita pe ramuri folosim functia display, functie ce traseaza o multime de structuri de tip plot. Sintaxa este:

> display (L, options);

unde L este o multime de structuri de tip plot.

Utilizarea functiei este obligatoriu precedata de instructiunea with(plots):

Exemplu:

Desenati graficul functiei

> with(plots): p1:=plot(x^3-3*x+2,x=-51,y=-104, axes =

normal): p2:=plot(ln(x+sqrt(x^2-1)),x=15,y=04,axes=normal):

display();

2. Spatii metrice

Distante

Utilizand Maple putem calcula distanta euclidiana dintre doua puncte din Rⁿ:

> with(student): distance (A,B);

Exemple:

Calculati distantele euclidiene dintre urmatoarele puncte, utilizand Maple

si ;

si .

> with(student):distance([1,3,5],[-4,0,1]);

> with(student):distance([1,3,5,5,8],[-4,0,1,2,1]);

2. Limite de siruri

Problema calcularii unor limite de siruri utilizand Maple este rezolvata, prin folosirea sintaxei yurmatoare:

> limit(f,n=infinity);

unde f este o functie de n.

Exemple:

Sa calculam utilizand  Maple urmatoarele limite:

, ,

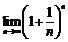
> limit(a^(1/n),n=infinity);

> limit(n^(1/n),n=infinity);

> limit((1+1/n)^n,n=infinity);

3. Serii

Pentru calculul sumei unei serii utilizand Maple folosim functia sum, cu urmatoarea sintaxa:

> sum (f,n = minfinity);

unde f este expresia, n este indicele de insumare, m numar natural.

Exemple:

Sa se calculeze suma urmatoarelor serii:

, ,

> sum((3*n^2+3*n+1)/(n*(n+1))^3,n=1infinity);

> sum((3^n+2^n)/6^n,n=0infinity);

4. Limite de functii   

Functia limit calculeaza limita unei expresii, a carei sintaxa este:

> limit (f, x = a, optiuni);

unde f este expresia, x = nume, a punctul in care se calculeaza limita care poate fi finit sau infinit iar argumentul optiuni poate fi left sau right.

Exemple:

Sa se verifice urmatoarele limite de functii:

> limit((1+x)^(1/x),x=0);

> limit((ln(1+x))/x,x=0);

5. Functii diferentiabile

(a) Functii de o singura variabila

Utilizand Maple, functia diff , care are urmatoarea sintaxa, calculeaza derivatele functiilor reale de o variabila reala:

> diff(f(x),x);

Exemple:

Calculati urmatoarele derivate:

,

> g:=diff(arcsin(2*x/(1+x^2)),x);

> h:=diff(sqrt(3*x+1),x);

(b) Functii de mai multe variabile (derivate partiale)

Pentru a calcula derivatele partiale utilizand Maple, folosim functia diff care calculeaza derivata partiala a unei expresii in raport cu variabila specificata, sintaxa fiind:

> diff( f,x_i);

unde

- f este o functie de variabile

- x_i este variabila in raport cu care se deriveaza

Exemple:

Calculati urmatoarele derivate partiale (in raport cu x si y):

,

> diff((x^2-y^2)/(x^2+x*y+y^2),x);

> diff((x^2-y^2)/(x^2+x*y+y^2),y);

> diff(ln(x+sqrt(x^2+y^2)),x);

> diff(ln(x+sqrt(x^2+y^2)),y);

6. Integrala Riemann

Pentru a calcula integrale utilizand Maple folosim functia int sau Int :

> int(expr, x=a..b, );

> Int(expr, x=a..b, );

unde expr - expresia algebrica a functiei de integrat, x - variabila si a, b - intervalul de integrare, apoi:

> evalf(%);

pentru obtinerea valorii.

Exemple:

Calculati integralele: , ,

> int(ln(x+sqrt(x^2+1)),x=01);

> evalf(%);

>int(x*arctan(x),x=-sqrt(3)0);

> evalf(%);

> int(x*ln((1-x)/(1+x)),x=-1/21/2);

> evalf(%);