Probleme de judecata

Oferim in cele ce urmeaza o selectie de probleme ce nu necesita cunostinte de matematica avansate (doar nivelul gimnazial) dar care pun la incercare capacitatea de judecata, inspiratia si creativitatea gindirii. Rezolvarea acestor probleme constituie un bun antrenament pentru cresterea capacitatii de gindire creativa precum si a fluiditatii gindirii. Credem ca nu degeaba aceste doua trasaturi sint considerate cele mai importante semne ale tineretii mintii.

Problemele, selectate din multiple surse, nu au putut fi grupate in ordinea dificultatii mai ales datorita diversitatii si varietatii lor. Ele au fost doar separate in citeva categorii a caror nume vrea sa sugereze un anumit mod de gindire pe care l-am folosit si noi in rezolvarea lor. Cele cu un grad mai mare de dificultate au fost marcate cu un semn (sau mai multe semne) de exclamare.

Criteriul principal pe baza caruia s-a facut aceasta selectie a fost urmatorul: fiecare problema cere in rezolvarea ei un minimum de inventivitate si creativitate. Majoritatea problemelor te pun 'fata in fata cu imposibilul', asa ca rezolvarea fiecarei probleme necesita depasirea unor 'limitari ale gindirii' plus un minimum de originalitate in gindire. Tocmai de aceea, pentru rezolvarea lor este nevoie de efort, putere de concentrare si perseverenta. Zis intr-un singur cuvint: este necesar si un strop de pasiune.

Consideram ca eforturile consecvente ale celor care vor rezolva aceste probleme vor fi din plin rasplatite prin placerea 'mintii biruitoare' si prin amplificarea calitatilor urmatoare: capacitate sporita de efort intelectual, putere de concentrare marita si prospetime in gindire.

Va dorim mult succes !

Probleme de perspicacitate

Stiind ca o sticla cu dop costa 1500 lei si ca o sticla fara dop costa 1000 lei, cit costa un dop ?

Stiind ca un ou costa 1000 lei plus o jumatate de ou, cit costa un ou ?

Ce numar lipseste alaturi de

ultima figura:

3 4 2 ?

Lui Popescu nici prin gind nu-i trecea sa foloseasca toate mijloacele pe care le avea la indemina ca sa lupte impotriva adversarilor tendintei contra neintroducerii miscarii anti-fumat. Care este pozitia lui Popescu: este pentru sau contra fumatului ?

Impartirea 'imposibila'. Sa se imparta numarul 12 in doua parti astfel incit fiecare parte sa fie 7.

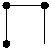
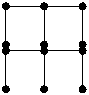
9 puncte. Sa se sectioneze toate cele 9 mici discuri cu o linie frinta neintrerupta (fara a ridica creionul de pe hirtie) compusa din 4 segmente. (!) Dar din trei segmente, este posibil ?

Trei cutii. In trei cutii identice sint inchise trei perechi de fructe: fie o pereche de mere, fie o pereche de pere, fie o pereche formata dintr-un mar si o para. Pe cele trei cutii sint lipite trei etichete: 'doua mere', 'doua pere' si, respectiv, 'un mar si o para'. Stiind ca nici una din etichete nu corespunde cu continutul cuitei inchise pe care se afla, sa se afle care este numarul minim de extrageri a cite un fruct pentru a se stabili continutul fiecarei cutii.

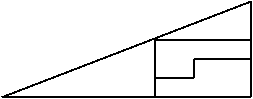
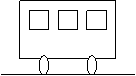
In ce directie merge autobuzul din desenul alaturat ?

(!) Intrerupatoarele. Pe peretele alaturat usei incuiate de la intrarea unei incaperi, se afla trei intrerupatoare ce corespund cu cele trei becuri de pe plafonul incaperii in care nu putem intra. Actionind oricare din intrerupatoare, dunga de lumina care apare pe sub usa ne asigura ca niciunul din cele trei becuri nu este ars. Cum putem afla, fara a patrunde in incapere, care intrerupator corespunde cu care bec ?

(!!) Cine muta ultimul cistiga. Doi jucatori dispun de o masa de joc de forma circulara sau patrata si de un numar mare de monezi identice. Ei muta plasind pe masa de joc in spatiul neocupat, fara suprapunere, cite o moneda alternativ pina cind unul dintre jucatori, care pierde in acest caz, nu mai poate plasa nicaieri o moneda. Sa se arate ca primul jucator are o strategie sigura de cistig.

(!!!) Iepurele si robotul-vinator. Intr-o incinta inchisa (un gen de arena) se afla un iepuras si un robot-vinator inzestrat cu clesti, mijloc de deplasare, calculator de proces si "ochi" electronici. Stiind ca viteza de deplasare a robotului-vinator este constanta si de zeci de ori mai mare decit a iepurasului, ce sanse mai are iepurasul de a scapa ?

Cintarul defect. Avind la dispozitie un cintar gradat defect care greseste constant cu aceeasi valoare (cantitate necunoscuta de grame), putem sa cintarim ceva determinindu-i corect greutatea ?

Jocul dubletilor (inventat de Carroll Lewis). Stiind ca trecerea de la un cuvint cu sens la altul cu sens este permisa doar prin modificarea unei singure litere odata (de exemplu: UNU UNI ANI ARI GRI GOI DOI ) se cere: Dovediti ca IARBA este VERDE si ca MAIMUTA a condus la OMENIRE, faceti din UNU DOI, schimbati ROZ-ul in ALB, puneti ROUGE pe OBRAZ si faceti sa fie VARA FRIG.

Impaturirea celor 8 patrate. Impaturiti initial in opt o foaie dreptunghiulara dupa care desfaceti-o si insemnati fiecare din cele opt zone dreptunghiulare obtinute (marcate de pliurile de indoire) cu o cifra de la 1 la 8. Puteti impaturi foaia  astfel obtinuta reducind-o de opt ori (la un singur dreptunghi sau patrat) astfel incit trecind cu un ac prin cele opt pliuri suprapuse acesta sa le perforeze exact in ordinea 1, 2, 3, . , 8 ? Incercati aceste doua configuratii:

Problema pentru cei puternici. Incercati sa impaturiti de 8 ori, pur si simplu, o coala de hirtie (de fiecare data linia de indoire este 'in cruce' peste cea dinainte). Este posibil ? (!)Determinati ce dimensiuni ar trebui sa aiba foaia la inceput pentru a putea fi impaturita de 8 ori.

Este posibil ca un cal sa treaca prin toate cele 64 de patratele ale unei table de sah, incepind dintr-un colt si terminind in coltul diagonal opus ?

Intr-un atelier exista 10 ladite ce contin fiecare piese cu greutatea de 100 grame, cu exceptia uneia din ladite ce contine piese avind grutatea de 90 grame. Puteti preciza care este ladita cu pricina, folosind un cintar doar pentru o singura data ?

Probleme cu chibrituri

(!) Eliminind un singur bat de chibrit ceea ce ramine in fata ochilor este un elipsoid!

(!) 9 bete. Sa se aseze 9 bete de chibrit astfel incit ele sa se intilnesca la virf tot cite trei in sase virfuri distincte.

De la 4 la 3. In figura ce contine 4 patrate, mutind 4 bete sa se obtina o figura ce contine doar 3 patrate.

Mutind doar un singur bat de chibrit sa se restabileasca egalitatea:

Problema ariilor intregi. Puteti aseza 12 chibrituri astfel incit ele sa formeze contururile unor poligoane ce au aria intreaga egala cu 5, (!!) 4, 3, 2, (!!!) 1 ? Se subintelege ca un chibrit poate fi asimilat cu un segment de lungime 1 si ca nu exista nici o dificultate de a forma 'din ochi' unghiuri drepte.

Probleme de logica si judecata

Substituirea literelor. Subtituiti literele cu cifre astfel incit urmatoarele adunari sa fie corecte: GERALD + DONALD = ROBERT ; FORTY + TEN + TEN = SIXTY ; BALON + OVAL = RUGBY.

Test de angajare la Microsoft. Patru excursionisti ajung pe malul unui riu pe care doresc sa-l traverseze. Intrucit s-a inoptat si ei dispun doar de o singura lanterna, ei pot sa treaca riul cel mult cite doi laolalta. Stiind ca, datorita diferentelor de virsta si datorita oboselii, ei ar avea individual nevoie pentru a traversa riul de 1, 2, 8 si 10 minute, se cere sa se decida daca este posibila traversarea riului in aceste condittii in doar 17 minute ?

(!) Imposibila. Sa se taie toate cele 16 segmente ale figurii urmatoare cu o singura linie curba continua si care nu se intersecteaza cu ea insasi.

(!) Problema 'ochilor albastri'. Sintem martorii urmatorului dialog intre doua persoane X si Y. << X: Eu am trei copii. Produsul virstei lor este 36 iar suma virstei lor este egala cu numarul de etaje al blocului din vecini de mine. Il stii, nu-i asa ? Y: Desigur. Dar numai din cit mi-ai spsus nu pot sa deduc care este virsta copiilor tai. X: Bine, atunci afla ca cel mare are ochi albastrii.>> Puteti afla care este virsta celor trei copii ?

Problema calugarului budhist. Intr-o dimineata, exact la rasaritul soarelui, un calugar budhist porneste de la templul de la baza muntelui pentru a ajunge la templul din virful muntelui exact la apusul soarelui, unde el se roaga toata noaptea. A doua zi el porneste din virf pe aceesi carare, tot la rasaritul soarelui, pentru a ajunge la templul de la baza muntelui exact la apusul soarelui. Sa se arate ca a existat un loc pe traseu in care calugarul s-a aflat in ambele zile exact la aceasi ora.

Vinul in apa si apa in vin. Dintr-o sticla ce contine un litru de apa este luat un pahar (un decilitru) ce este turnat pest un litru de vin. Vinul cu apa se amesteca bine dupa care se ia cu acelasi pahar o cantitate egala de 'vin cu apa' ce se toarna inapoi peste apa din sticla. Avem acum mai multa apa in vin decit vin in apa, sau invers ?

(!!!!) Cuiele in echilibru. Avem la dispozitie 7 cuie normale, cu capul obisnuit. Infigem unul vertical in podea (sau intr-o placa de lemn). Se cere sa se aseze cele 6 cuie ramase in echilibru stabil pe capul cuiului vertical, fara ca niciunul din cele sase cuie sa atinga podeaua.

(!!) Tigarile tangente. Este posibil sa asezam pe masa sase tigari astfel incit fiecare sa se atinga cu fiecare (oricare doua sa fie tangente) ? (!!!) Dar sapte tigari ?

(!) Problema celor 12 intelepti (in varianta moderna). Managerul unei mari companii doreste sa puna la incercare inteligenta si puterea de judecata a celor 12 membrii ai consiliului sau de conducere. Luind 12 carti de joc, unele de pica si altele de caro, el le aseaza cite una pe fruntea fiecarui consilier astfel incit fiecare sa poata vedea cartile de pe fruntile celorlalti dar nu si pe a sa. Managerul le cere celor care considera ca au pe frunte o carte de caro (diamond) sa faca un pas in fata, altfel ei nu vor mai putea face parte din consiliu. Dupa ce isi repeta cererea de sapte ori, timp in care niciunul din cei 12 consilieri nu face nici o miscare (ci doar se privesc unii pe altii), toti consilierii care au intr-adevar pe frunte o carte de caro ies deodata in fata. Puteti deduce citi au iesit si cum si-au dat ei seama ce carte este asezata pe fruntea lor ?

Paianjenul si musca. Pe peretele lateral al unei hale cu dimensiunile de 40 x 12 x12 metri, pe linia mediana a peretelui lateral si exact la 1 metru de tavan, se afla un paianjen. Pe peretele lateral opus, tot pe linia mediana si exact la 1 metru de podea, se afla o musca amortita. Care este distanta cea mai scurta pe care paianjenul o are de parcurs de-a lungul peretilor pentru a se infrupta din musca ?

Rifi si Ruf. Cei doi iubiti Rifi si Ruf, din nordica tara Ufu-Rufu, locuiesc in sate diferite aflate la distanta de 20 km unul de altul. In fiecare dimineata ei pornesc exact deodata (la rasarit) unul spre celalalt spre a se intilni si a se saruta confrom obiceiului nordic: nas in nas. Intr-o dimineata o musca ratacita porneste exact la rasaritul soarelui de pe nasul lui Rifi direct spre nasul lui Ruf, care o alunga trimitind-o din nou spre nasul lui Rifi, s.a.m.d. , pina cind ea sfirseste tragic in momentul 'sarutului' celor doi. Stiind ca Rifi se deplaseaza cu 4 km/ora, Ruf cu 6 km/ora iar musca zboara cu 10 km/ora, se cere sa se afle ce distanta a parcurs musca in zbor de la rasarit si pina in momentul tragicului ei sfirsit.

O anti-problema de sah. In urmatoarea configuratie a pieselor pe o tabla de sah se cere sa nu dati mat dintr-o mutare ! (Albul ataca de jos in sus. Legenda: P-pion, N-nebun, R-rege, T-turn, C-cal. Alaturat fiecarei piese este scrisa culoarea sa, alb-a sau negru-n.)

Bronx contra Brooklyn. Un tinar, ce locuieste in Manhattan in imediata apropiere a unei statii de metrou, are doua prietene, una in Brooklyn si cealalta in Bronx. Pentru a o vizita pe cea din Brooklyn el ia metroul ce merge spre partea de jos a orasului, in timp ce, pentru a o vizita pe cea din Bronx, el ia din acelasi loc metroul care merge in directie opusa. Metrourile spre Brooklyn si spre Bronx intra in statie cu aceesi frecventa: din 10 in 10 minute fiecare. Dar, desi el coboara in statia de metrou in fiecare simbata la intimplare si ia primul metrou care vine (nedorind sa 'favorizeze' pe nici una din prietenele sale), el a constatat ca, in medie, el merge in Brooklyn de 9 ori din 10. Puteti gasi o explicatie logica a fenomenul ?

(!!) Problema celor 12 bile. In fata noastra se afla 12 bile identice ca forma, vopsite la fel, dar una este cu siguranta falsa, ea fiind fie mai grea, fie mai usoara, fiind facuta dintr-un alt material. Avem la dispozitie o balanta si se cere sa determinam doar prin 3 cintariri care din cele 12 bile este falsa precizind si cum este ea: mai grea sau mai usoara. (!!!) Mai mult, puteti determina care este numarul maxim de bile din care prin 4 cintariri cu balanta se poate afla exact bila falsa si cum este ea ?

(!) Problema celor 2 perechi de manusi. Aflat intr-o situatie ce implica interventia de urgenta, un medic chirurg constata ca are la dispozitie doar 2 perechi de manusi sterile desi el trebuie sa intervina rapid si sa opereze succesiv 3 bolnavi. Este posibil ca cele trei operatii de urgenta sa se desfasoare in conditii de protectie normale cu numai cele 2 perechi de manusi ? (Singele fiecaruia din cei 3 pacienti, precum si mina doctorului nu trebuie sa conduca la un contact infectios.)

(!!) Problema fringhiei prea scurte. O persoana ce are asupra ei doar un briceag si o fringhie lunga de 30 metri se afla pe marginea unei stinci, privind in jos la peretele vertical de 40 metri aflat sub ea. Fringhia poate fi legata doar in virf sau la jumatatea peretelui (la o inaltime de 20 metri de sol) unde se afla o mica platforma de sprijin. Cum este posibil ca persoana aflata in aceasta situatie sa ajunga teafara jos coborind numai pe fringhie, fara a fi nevoita sa sara deloc punindu-se astfel in pericol ?

Problema luminarilor neomogene. Avem la dispozitie chibrite si doua luminari care pot arde exact 60 minute fiecare insa, ele fiind neomogene, nu vor arde cu o viteza constanta. Cum putem masura precis o durata de 45 minute ?

(!!) O jumatate de litru. Avem in fata noastra un vas cilindric cu capacitatea de 1 litru, plin ochi cu apa. Se cere sa masuram cu ajutorul lui ½ litru de apa, fara a ne ajuta de nimic altceva decit de miinile noastre.

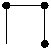
(!) Sa vezi si sa nu crezi. Priviti urmatoarele doua figuri: prin reasezarea decupajelor interioare ale primeia se obtine din nou aceeasi figura dar avind un patratel lipsa ! Cum explicati 'minunea' ?

Probleme de logica si judecata cu 'tenta informatica'

(!!!) Decriptarea scrierii incifrate. Se dau urmatoarele numere impreuna cu denumirile lor cifrate:

Care este regula de incifrare? Ce numere reprezinta urmatoarele coduri cifrate: nagevonagevogedunanabivobiduvogedu; 

nagevonaduvogedunanabivobiduvogedu;

naduvogenanabivobiduvogedu;

nanabivogeduvogedu;

nabivonabivonaduvogedunagevonagevogedunanabivobiduvogedu;

nanagevobiduvogedu?

Incifrati numerele 256 si 1024 prin acesta metoda.

(!!!) Altfel de codificare binara a numerelor. Descoperiti metoda de codificare binara a numerelor folosita in continuare:

Puteti spune ce numere sint codificate prin 100, 101, 1000, 1111, 10000 si 11111 ? Puteti codifica numerele 70, 80, 90, 100, 120, 150 si 1000 ?

(!!!) Problema dialogului perplex. Exista doua numere m si n din intervalul [2..99] si doua persoane P si S astfel incit persoana P stie produsul lor, iar S stie suma lor. Stiind ca intre P si S a avut loc urmatorul dialog:

'Nu stiu numerele' spune P.

'Stiam ca nu stii' raspunde S, 'nici eu nu stiu.'

'Acuma stiu !' zice P stralucind de bucurie.

'Acum stiu si eu . ' sopteste satisfacut S.

sa se determine toate perechile de numere m si n ce 'satisfac' acest dialog (sint solutii ale problemei).

(!!!!) Impaturirea celor 8 patrate. Impaturiti initial in opt o foaie dreptunghiulara dupa care desfaceti-o si insemnati fiecare patratel obtinut cu o cifra de la 1 la 8. Proiectati un algoritm si realizati un program care, primind configuratia (numerotarea) celor 8 patratele, sa poata decide daca se poate impaturi foaia astfel obtinuta reducind-o de opt ori (la un singur patrat) astfel incit trecind cu un ac prin cele opt foi suprapuse acesta sa le perforeze exact in ordinea 1, 2, 3, . , 8.

(!!!!) Problema fetelor de la pension. Problema a aparut pe vremea cind fetele invatau la pension fara ca prin prezenta lor baietii sa le tulbure educatia. Pedagoaga fetelor unui pension de 15 fete a hotarit ca in fiecare dupa-amiaza, la ora de plimbare, fetele sa se plimbe in cinci grupuri de cite trei. Se cere sa se stabileasca o programare a plimbarilor pe durata unei saptamini (sapte zile) astfel incit fiecare fata sa ajunga sa se plimbe numai o singura data cu oricare din celelalte paisprezece (oricare doua fete sa nu se plimbe de doua ori impreuna in decursul unei saptamini).