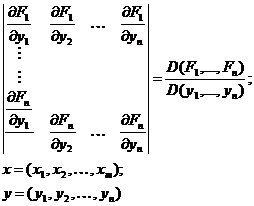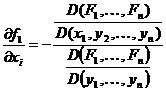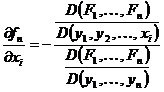Sisteme de functii implicite
Se considera sistemul de functii implicite:
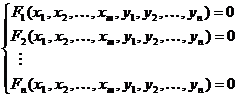 (A.4.30)
(A.4.30)
unde Fi(x1,x2, .
. . ,xm, y1, y2, . . . ,yn), 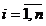 , sunt functii reale de (m+n) variabile definite pe o multime E Rm+n
, sunt functii reale de (m+n) variabile definite pe o multime E Rm+n
Definitie:
Spunem ca un sistem de n
functii reale de m variabile:
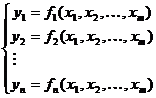 (A.4.31)
(A.4.31)
definite pe
multimea A Rm este o solutie a sistemului (A.4.30) in raport cu variabilele y1, y2, . . . , yn
pe multimea A daca
avem:
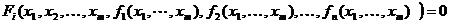
oricare ar fi i =1,2,. . . ,n, pentru (x1, x2, . . . , xm)IA.
In cazul cand sistemul (A.4.30) are o singura
solutie pe A spunem ca
functiile f1,f2,
. . . ,fn sunt definite implicit pe sistemul de ecuatii
(A.4.30).
Sa presupunem ca functiile F1, F2, . . . , Fn
au derivate partiale in raport cu variabilele y1, y2, . . . , yn pe
multimea E.
Vom nota:
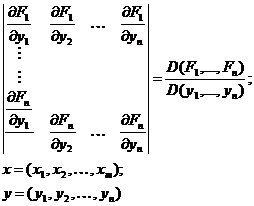
Daca
mai notam: F=(F1,F2,
. . ,Fn) atunci F este
o functie vectoriala definita pe E cu valori in Rn
, iar sistemul (A.4.30) se scrie:
F(x,z)=0 (A.4.32)
De
asemenea, daca notam f=(f1,f2,
. . . ,fn), atunci f
este o functie vectoriala definita pe A Rm cu valori in Rn, iar
sistemul (A.4.31) se scrie:
y=f(x) . (A.4.33)
A spune
ca sistemul (A.4.31) este o solutie a sistemului (A.4.30) este
echivalent cu:
F(x,f(x))=0 (A.4.34)
pentru orice xIA
Teorema: Fie E Rm+n si 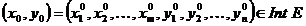 ; fie functia vectoriala F=(F1,F2, . . . ,Fn):E Rn
; fie functia vectoriala F=(F1,F2, . . . ,Fn):E Rn
Daca:
1) F(x0,y0)=0;
2) Functiile reale Fi(i=1,2,. . . ,n) au
derivate partiale continue  intr-o vecinatate
U0 V0 a punctului (x0,y0);
intr-o vecinatate
U0 V0 a punctului (x0,y0);
3) Iacobianul:
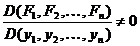
in punctul (x0,y0).
Atunci:
a)Exista o vecinatate U0 V0 a punctului (x0,y0),
(U0 Rm,V0 Rn) si o functie vectoriala unica f(x)=(f1(x), . . . , fn(x)):U0 V0, astfel incat y0=f(x0) si F(x,f(x))=0 pentru orice xIU0
b)Functiile reale f1(x),f2(x), . . . , fn(x) au
derivate partiale continue pe U0
si:
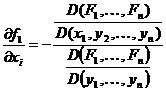
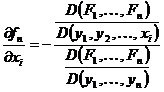
c)Daca functiile F1,F2, . . . , Fn au derivate
partiale de ordinul k continue
pe U V,
atunci functiile f1(x), f2(x),
. . . , fn(x) au derivate partiale de ordinul k continue pe U0.


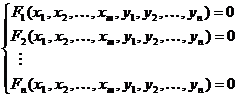 (A.4.30)
(A.4.30)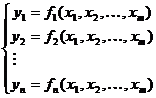 (A.4.31)
(A.4.31)