Tipuri de structuri

Tipuri de structuri

Arcul   Grinda cu zabrele

Arc liniar incarcat cu o forta concentrata: Adaugarea unui tirant conduce la

reactiunile au o componenta orizontala preluarea reactiunii orizontale din

importanta care tinde sa "indeparteze" reazeme si realizarea unei grinzi

reazemele.    cu zabrele.

Fortele in grinzi cu zabrele

Grinzile cu zabrele sunt formate din elemente dublu articulate. Prin urmare ele pot dezvolta doar eforturi axiale (eforturi normale).

Reazemele:

-unul dintre ele este articulat, permitand rotirea libera datorata schimbarii (minore) a formei grinzii cu zabrele datorita incarcarii

-un reazem cu role (reazem simplu), care permite rotirea libera si miscarea laterala orizontala provenita din incarcari si schimbarile de temperatura

Fortele in grinzile cu zabrele:

-tirantiisunt supusi la intindere(+)

-grinzile diagonalesunt comprimate(-)

Daca sunt aplicate mai multe forte

pe lungimea unei grinzi,

aceasta este supusa

eforturilor de incovoiere

Pentru a evita eforturile de incovoiere,

pot fi adaugate

elemente diagonalesi montanti

verticali

In cazul deschiderilor

mari ale grinzilor cu zabrele

pot fi adaugate mai multe elemente diagonale

si montanti verticali

pentru a evita eforturile de incovoiere

Forma alternativa a unei grinzi cu zabrele

Pentru o anumita incarcare se poate gasi forma unui arc liniar (forma parabolica)

Pentru a prelua forta orizontala din reazeme este adaugat un tirant

Rezulta o forma instabila

(in principal din cauza variatiei fortelor)

Pentru a oferi stabilitate talpilor superioare si inferioare

ale grinzii cu zabrele (articulate la capete),

sunt dispuse diagonale si montanti.

Daca forma arcului corespunde unui arc liniar,

elementele interne sunt nesolicitate,

insa acestea sunt esentiale pentru stabilitatea grinzii cu zabrele

Grinda cu zabrele tip arc inversat

avantaje: elementele lungi sunt intinse

dezavantaje: inaltime libera mai mica

Forme ale grinzilor cu zabrele

Forma curba a arcelor: dificil de fabricat grinzile cu zabrele sunt realizate cel mai adesea cu talpi paralele.

Grinzi cu zabrele cu talpi paralele conduc la necesitatea folosirii elementelor de inima (diagonale si montanti), care transmit fortele intre cele doua talpi.

Grinda cu zabrele Pratt

-talpa superioara este comprimata;

-talpa inferioara si diagonalele sunt intinse;

-o proiectare economica presupune ca elementele

cele mai lungi sa fie intinse (diagonalele)

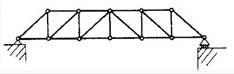Grinda cu zabrele tip Howe

-talpa superioara este comprimata;

talpa inferioara este intinsa;

-diagonalele sunt comprimate.

Grinda cu zabrele tip Warren

talpa superioara este comprimata;

talpa inferioara este intinsa;

diagonalele sunt pe rand intinse si comprimate;

economia de fabricatie: toate elementele au aceeasi

lungime si imbinarile au aceeasi configuratie.

Nodurile grinzilor cu zabrele

Nodurile articulate conduc la

structuri static determinate eforturile

din elemente pot fi determinate doar

din relatiile de echilibru.

Nodurile rigide provoaca

eforturi mici de incovoiere,

dar acestea pot fi neglijabile datorita

formei triunghiulare a panourilor.

In mod traditional grinzile cu zabrele

sunt proiectate cu noduri articulate,

chiar daca elementele au legaturi rigide intre ele.

Grinzi cu zabrele spatiale

Cea mai uzuala grinda cu zabrele plana consta dintr-o serie de triunghiuri.

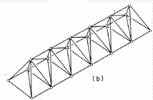Forma corespunzatoare in spatiu este cea a tetraedronului(a).

Grinda cu zabrele schitata in (b) este o grinda cu zabrele spatiala:

in mod teoretic este economica in folosirea materialului;

Nodurile sunt dificil de realizat si de obicei foarte scumpe

Solutia pentru grinzi cu zabrele care sa ofere spatiu de circulare:

doua grinzi cu zabrele plane cu traverse.

Grinzi cu zabrele static nedeterminate

Exista o varietate mare de grinzi cu zabrele static nedeterminate

Exemple(a): diagonalele duble in mijlocul panoului. In consecinta una din diagonale va fi tot timpul intinsa

Exemplu(b): Podul portului din Sydney, Australia (Sydney Harbour Bridge), cu ambele reazeme articulate

Grinzi

Grinda: structura care sustine incarcarile prin abilitatea de a rezista eforturilor de incovoiere.

Leonardo daVinci (1452-1519): rezistenta unei grinzi din lemn este proportionala cu patratul inaltimii ei.

Leonhard Euler si Daniel Bernoulli au fost primii care au reusit sa formuleze o teorie realista, in jurul anului 1750

Grinzi: analogie cu grinzile cu zabrele

Fortele intr-o grinda Pratt, incarcata cu o forta centrala:

Fortele intr-o grinda Howe:

Fortele intr-o

grinda cu zabrele

cu diagonale duble

(estimare):

Talpile:

fortele din elementele talpilor superioare si inferioare din fiecare panou sunt egale, dar de semne diferite, iar ele cresc cu distanta de la reazemul cel mai apropiat;

-talpile trebuie sa reziste momentelor incovoietoare, in mod proportional cu distanta de la reazemul cel mai apropiat.

Diagonalele:

-fortele din diagonale sunt egale, dar cu semne opuse si au aceeasi valoare in toate panourile;

-diagonalele vor rezista fortelor de forfecare , aceeasi pentru toate panourile.

Deformatii de incovoiere si forfecare in grinzile cu zabrele

Grinzi cu inima plina (din otel)

Grinzile cu inima plina din otel: au talpi puternice si inimi subtiri, sudate si rigidizate prin rigidizari transversale.

Pentru o forta unitara aplicata la mijlocul deschiderii:

- talpa superioara este comprimata;

- talpa inferioara este intinsa;

- inima este supusa la forfecare, eforturile fiind similare cu cele ale diagonalelor din grinzile cu zabrele.

Dupa voalarea inimii,aceasta mai poate prelua decat fortele de intindere, grinda actionand ca o grinda cu zabrele tip Pratt.

Grinzi: incovoiere

Talpa superioara este comprimata

Talpa inferioara este intinsa

Tensiunea normala este proportionala cu distanta fata de axa neutra

Simplificari:

-Inima este subtire, talpile sunt groase inima are o contributie minora la rezistenta la incovoiere

(poate fi ignorata)

-Efortul normal poate fi considerat uniform pe grosimea talpilor

Capacitatea de rezistenta la moment incovoietor:

-Grinda dublu T idealizata: M = σ A d/2

-Grinda rectangulara cu

aceeasi arie si inaltime: M = σ b d2/6 = σ A d/6

Pentru cazul de incovoiere,

cea mai buna dispunere a materialului

este cat mai departe de axa neutra

Exemple de pozitionare eficienta a materialului pentru rezistenta la incovoiere

-Grinzi usoare de acoperis(grinzi cu zabrele) Grinzi laminate la cald

sau reconstituite prin sudare

Exemple de pozitionare eficienta a materialului pentru rezistenta la incovoiere

Exemple de pozitionare eficienta a materialului pentru rezistenta la incovoiere

-Table profilate din otel

Grinzi ajurate

-Stalpi care necesita rezistenta la incovoiere pe orice directie: sectiunile tubulare

Grinzi: forfecare

Grinzile simplu rezemate cu sectiune transversala rectangulara si uniforma, incarcate cu o forta concentrata centrala W:

Pot rezista unui moment incovoietor:M = σ b d2/6;

prezinta o sageataδ.

Daca grinda este taiata in doua parti longitudinale in lungul planului neutru:

Are loc o alunecare relativa intre cele doua grinzi suprapuse;

cele doua grinzi nou formate vor prelua un moment incovoietor; M = 2 b (d/2)2/6] = σ b d2/12, jumatate din cel al grinzii intregi;

sageata grinzilor suprapuse este 4δ.

In cazul grinzii netaiate sunt prezente eforturi in lungul planului neutru pentru a preveni alunecarea celor doua jumatati de grinda: acestea sunt eforturile de forfecare.

Eforturile de mentinere a unitatii actiunii sunt mai mici mai sus si mai jos de planul neutru.

Eforturile de forfecare:

-au o variatie parabolica intr-o sectiune dreptunghiulara;

-sunt preluate in principal de inima grinzii si pot fi considerate constante pe inaltimea grinzii pentru o grinda dublu T din otel

Forme structurale

Grinda simplu rezemata supusa

fortelor uniform distribuite:

folosirea 'perfecta' a materialului pentru

rezistenta la incovoiere intr-o grinda cu

sectiune idealizata dublu T(M = σ A d/2):

variatie parabolica pe inaltime

Grinda simplu rezemata

supusa unei forte uniform distribuite

Folosirea 'perfecta' a materialului

pentru rezistenta la incovoiere intr-o

grinda cu sectiune transversala

idealizata dublu T(M = σA d/2):

variatie parabolica a inaltimii

Pod cu o deschidere centrala simplu rezemata si doua reazeme in consola;

Forma grinzii cu zabrele trebuie sa semene diagramei de moment incovoietor

pentru a face eficienta folosirea materialului din talpile superioare si inferioare.

Podul de cale ferata de la Quebec(Quebec railway bridge)

Forth bridge, Scotia

Podul Angel Saligny, Romania